题目内容
 如图,已知∠A=∠B,AA1,PP1,BB1均垂直于A1B1,AA1=17,PP1=16,BB1=20,A1B1=12,则AP+PB等于
如图,已知∠A=∠B,AA1,PP1,BB1均垂直于A1B1,AA1=17,PP1=16,BB1=20,A1B1=12,则AP+PB等于
- A.12
- B.13
- C.14
- D.15
B
分析:如图,AA1,PP1,BB1均垂直于A1B1,过点P作PF⊥AA1,交AA1于点D,交BB1于点F,延长BP交AA1于点C,作CG⊥BB1,交BB1于点G,然后根据矩形和直角三角形的性质求解.
解答: 解:如图,AA1,PP1,BB1均垂直于A1B1,
解:如图,AA1,PP1,BB1均垂直于A1B1,
∴AA1∥PP1∥BB1,
过点P作PF⊥AA1,交AA1于点D,交BB1于点F,延长BP交AA1于点C,作CG⊥BB1,交BB1于点G,
∴四边形DFB1A1,DPP1A1,FPP1B1,FDGC,CGB1A1是矩形,
∴DA1=PP1=FB1=16,CG=A1B1=12,
∵AA1∥BB1,
∴∠B=∠ACB,
∵∠A=∠B
∴∠A=∠BCA,
∴AP=CP,
∵PF⊥AA1,
∴点D是AC的中点,
∵AA1=17,
∴AD=CD=17-16=1,BF=20-16=4,FG=CD=1,BG=4+1=5,
∴BP+PA=BP+PC=BC=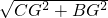 =
= =13.
=13.
故选B.
点评:本题通过作辅助线,构造矩形和直角三角形,利用矩形和直角三角形的性质和勾股定理求解.
分析:如图,AA1,PP1,BB1均垂直于A1B1,过点P作PF⊥AA1,交AA1于点D,交BB1于点F,延长BP交AA1于点C,作CG⊥BB1,交BB1于点G,然后根据矩形和直角三角形的性质求解.
解答:
 解:如图,AA1,PP1,BB1均垂直于A1B1,
解:如图,AA1,PP1,BB1均垂直于A1B1,∴AA1∥PP1∥BB1,
过点P作PF⊥AA1,交AA1于点D,交BB1于点F,延长BP交AA1于点C,作CG⊥BB1,交BB1于点G,
∴四边形DFB1A1,DPP1A1,FPP1B1,FDGC,CGB1A1是矩形,
∴DA1=PP1=FB1=16,CG=A1B1=12,
∵AA1∥BB1,
∴∠B=∠ACB,
∵∠A=∠B
∴∠A=∠BCA,
∴AP=CP,
∵PF⊥AA1,
∴点D是AC的中点,
∵AA1=17,
∴AD=CD=17-16=1,BF=20-16=4,FG=CD=1,BG=4+1=5,
∴BP+PA=BP+PC=BC=
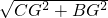 =
= =13.
=13.故选B.
点评:本题通过作辅助线,构造矩形和直角三角形,利用矩形和直角三角形的性质和勾股定理求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 =2,∠ADC=30°
=2,∠ADC=30° 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=