题目内容
 如图,在锐角△ABC中,AC是最短边,以AC中点O为圆心,
如图,在锐角△ABC中,AC是最短边,以AC中点O为圆心, AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连接AD、DC.若∠DAO=65°,则∠B+∠BAD=________.
AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连接AD、DC.若∠DAO=65°,则∠B+∠BAD=________.
65°
分析:由半径OA=OD得出∠ADO=∠DAO=65°,由三角形内角和定理求∠AOD的度数,由OD∥BC,得∠ACB=∠AOD,在△ABC中,再由内角和定理求∠B+∠BAD.
解答:∵OA=OD,∴∠ADO=∠DAO=65°,
∴在△AOD中,∠AOD=180°-∠ADO-∠DAO=50°,
又∵OD∥BC,
∴∠ACB=∠AOD=50°,
在△ABC中,∠B+∠BAD=180°-∠ACB-∠DAO=180°-50°-65°=65°,
故答案为:65°.
点评:本题考查了相似三角形的判定与性质.关键是由半径相等证等腰三角形,由三角形内角和定理求角的和.
分析:由半径OA=OD得出∠ADO=∠DAO=65°,由三角形内角和定理求∠AOD的度数,由OD∥BC,得∠ACB=∠AOD,在△ABC中,再由内角和定理求∠B+∠BAD.
解答:∵OA=OD,∴∠ADO=∠DAO=65°,
∴在△AOD中,∠AOD=180°-∠ADO-∠DAO=50°,
又∵OD∥BC,
∴∠ACB=∠AOD=50°,
在△ABC中,∠B+∠BAD=180°-∠ACB-∠DAO=180°-50°-65°=65°,
故答案为:65°.
点评:本题考查了相似三角形的判定与性质.关键是由半径相等证等腰三角形,由三角形内角和定理求角的和.

练习册系列答案
相关题目
 如图,在锐角△ABC中,以BC为直径的半圆O分别交AB,AC与D、E两点,且cosA=
如图,在锐角△ABC中,以BC为直径的半圆O分别交AB,AC与D、E两点,且cosA=
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
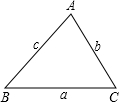 如图,在锐角△ABC中,a>b>c,以某任意两个顶点为顶点作矩形,第三个顶点落在以这两个顶点所确定的对边上,这样可以作三个面积相等的矩形,请问这三个矩形的周长大小关系如何?(记ta、tb、tc分别以a、b、c为边的矩形的周长)答:
如图,在锐角△ABC中,a>b>c,以某任意两个顶点为顶点作矩形,第三个顶点落在以这两个顶点所确定的对边上,这样可以作三个面积相等的矩形,请问这三个矩形的周长大小关系如何?(记ta、tb、tc分别以a、b、c为边的矩形的周长)答: 25、如图,在锐角△ABC中,AB>AC,AD⊥BC于D,以AD为直径的⊙O分别交AB,AC于E,F,连接DE,DF.
25、如图,在锐角△ABC中,AB>AC,AD⊥BC于D,以AD为直径的⊙O分别交AB,AC于E,F,连接DE,DF.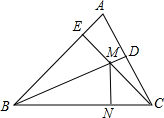 如图,在锐角△ABC中,∠ABC的平分线交AC于点D,AB边上的高CE交BD于点M,过点M作BC的垂线段MN,若EC=4,∠BCE=45°,则MN=
如图,在锐角△ABC中,∠ABC的平分线交AC于点D,AB边上的高CE交BD于点M,过点M作BC的垂线段MN,若EC=4,∠BCE=45°,则MN=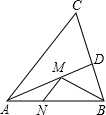 如图,在锐角△ABC中,AB=4,∠BAC=45°.∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点.则BM+MN的最小值是
如图,在锐角△ABC中,AB=4,∠BAC=45°.∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点.则BM+MN的最小值是