题目内容
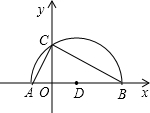
已知:如图,平面直角坐标系中,半圆的直径AB在x轴上,圆心为D.半圆交y轴于点C,AC=2 ,
, BC=4
BC=4 .
.
(1)证明:△AOC∽△ACB;
(2)求以AO、BO两线段长为根的一元二次方程;
(3)求图象经过A、B、C三点的二次函数的表达式;
(4)设此抛物线的顶点为E,连接EC,试判断直线EC与⊙O的位置关系,并说明理由.
 (1)证明:∵AB为半圆O的直径,
(1)证明:∵AB为半圆O的直径,∴∠ACB=90°.
∴∠AOC=∠ACB,∠CAO=∠BAC.
∴△AOC∽△ACB.
(2)解:AB=
 =10,
=10,∵△AOC∽△ACB,
∴
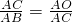 .
.∴AO=
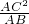 =2,BO=AB-AO=8.
=2,BO=AB-AO=8.∴以AO、BO两线段长为根的一元二次方程为( x-2 )( x-8 )=0;
(3)解:在Rt△AOC中,OC=4,
∴A(-2,0),B(8,0),C(0,4).
设经过A、B、C三点的二次函数的解析式为y=ax2+bx+c(a≠0),依题意有:
∴
 ,
,∴

∴表达式为:y=-
 x2+
x2+ x+4.
x+4.(4)直线EC与⊙D相切,理由如下:
∵
 ,
,∴顶点E的坐标为(3,
 ).
).连接EC、CD、ED,则CD=AD=5,ED=
 .
.∴CF=3,EF=
 ,CE=
,CE= .
.∴CD2+CE2=
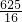 ,DE2=
,DE2=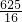 .
.∴CD2+CE2=DE2.
∴∠DCE=90°,CD为半径.
∴直线EC与⊙D的位置关系是相切.
分析:(1)根据圆的知识求出∠AOC=∠ACB,∠CAO=∠BAC然后可证明△AOC∽△ACB.
(2)由1得出相似三角形继而求出线段比.求出AO=
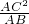 =2得解.
=2得解.(3)设经过A、B、C三点的二次函数的解析式为y=ax2+bx+c,把已知坐标代入求出函数表达式.
(4)把函数表达式化简求出点E的坐标,然后连接EC,CD,ED,根据勾股定理求证∠DCE=90°,即可知直线EC与⊙D的位置关系是相切.
点评:本题考查的是二次函数与圆的知识相结合的有关知识以及勾股定理的运用.难度较大.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 BC=4
BC=4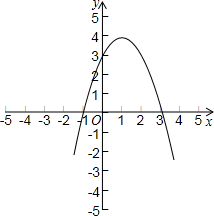 、B,其中点B在点A的右侧,抛物线图象与y轴交于点C,且经过点D(2,3).
、B,其中点B在点A的右侧,抛物线图象与y轴交于点C,且经过点D(2,3). 已知:如图在平面直角坐标系xOy中,直线AB分别与x,y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OA=3,OB=6,OE=2.
已知:如图在平面直角坐标系xOy中,直线AB分别与x,y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OA=3,OB=6,OE=2.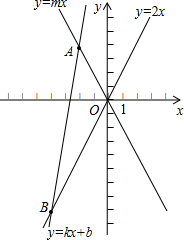 已知:如图,平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).
已知:如图,平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).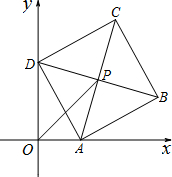 已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动,顶点D在y轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.
已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动,顶点D在y轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.