题目内容
.如图,半圆D的直径AB=4,与半圆O内切的动圆O1与AB切于点M,设⊙O1的半径为y,AM=x,则y关于x的函数关系式是 ( )
A.y=- x2+x x2+x | B.y=-x2+x | C.y=- x2-x x2-x | D.y= x2-x x2-x |
A
解析试题分析:解:O1M,OO1且延长OO1交圆与C,∵⊙O1与⊙O内切,∴,O1M⊥AO,又AB=4,O1M=x,⊙O1的半径为y∴OM=2-x,OO1=2-y,在Rt△OO1M中,(2-y)2-y2=(2-x)2,解得y=- x2+x.
x2+x.
考点:切线定理,勾股定理。
点评:熟知以上两定理,在解题时,x与y可利用直角三角形勾股定理解得,把三边的长用x,y来表示,本题由一定的难度,做辅助线是解题的关键,属于中档题。

练习册系列答案
相关题目
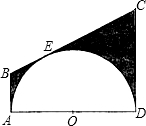 如图,半圆O的直径AD=12cm,AB,BC,CD分别与半圆O切于点A,E,D.
如图,半圆O的直径AD=12cm,AB,BC,CD分别与半圆O切于点A,E,D.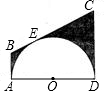 如图,半圆O的直径AD=12cm,AB、BC、CD分别与半圆O切于点A、E、D.
如图,半圆O的直径AD=12cm,AB、BC、CD分别与半圆O切于点A、E、D.
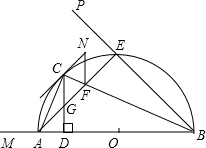 N∥CD,过C作圆的切线交FN于N.
N∥CD,过C作圆的切线交FN于N. 如图,半圆O的直径为6cm,∠BAC=30°,则阴影部分的面积是( )
如图,半圆O的直径为6cm,∠BAC=30°,则阴影部分的面积是( ) 如图,半圆O的直径AB=20,将半圆O绕点B顺针旋转45°得到半圆O′,与AB交于点P.
如图,半圆O的直径AB=20,将半圆O绕点B顺针旋转45°得到半圆O′,与AB交于点P.