题目内容
12.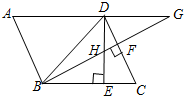 如图,平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE,BF相交于H,BF,AD的延长线相交于G,下面结论:①DB=$\sqrt{2}$BE,②△BHE∽△BCF,③AB=BH,④△BHD∽△BDG,其中正确的结论是( )
如图,平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE,BF相交于H,BF,AD的延长线相交于G,下面结论:①DB=$\sqrt{2}$BE,②△BHE∽△BCF,③AB=BH,④△BHD∽△BDG,其中正确的结论是( )| A. | ①②③④ | B. | ①②③ | C. | ①②④ | D. | ②③④ |
分析 ①由题意可知△BDE是等腰直角三角形,故此可得到BD=$\sqrt{2}$BE,②由∠HBE=∠CBF,∠HEB=∠CFB证明即可;③先证明△BHE≌△DEC,从而得到BH=DC,然后由平行四边形的性质可知AB=BH;④由∠BDH≠∠G可知△BHD与△BDG不相似.
解答 解:①∵∠DBC=45°,DE⊥BC于E,
∴BD=$\sqrt{2}$BE,故①正确;
②∵∠HBE=∠CBF,∠HEB=∠CFB,
∴△BHE∽△BCF,故②正确.
③∵∠DBC=45°,DE⊥BC于E,
∴∠DBC=∠BDE=45°.
∴DE=BE.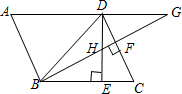
由②可知:△BHE∽△BCF,
∴∠BHE=∠DCE.
在△BHE和△DCE中,$\left\{\begin{array}{l}{∠BHE=∠DCE}\\{∠BEH=∠DEC}\\{BE=DE}\end{array}\right.$,
∴△BHE≌△DCE.
∴BH=DC.
∵四边形ABCD为平行四边形,
∴AB=DC.
∴AB=BH,故③正确.
④在△BHD和△BDG中,∠DBH=∠DBG,但是两锐角:∠BDH≠∠G,故△BHD与△BDG不相似,故④错误.
故选:B.
点评 本题主要考查的是相似三角形的性质和判定、全等三角形的性质和判定、特殊锐角三角函数值,平行四边形的性质,熟练掌握相关性质是解题的关键.

练习册系列答案
相关题目
3.下列说法正确的是( )
| A. | 一个数的倒数等于它本身,则这个数是±1,0 | |
| B. | 一个数的相反数等于它本身,则这个数一定是0,1 | |
| C. | 一个数的绝对值等于它本身,则这个数一定是正数 | |
| D. | 一个数的平方等于1,则这个数是±1 |
17.已知1是关于x的一元二次方程x2+(m-1)x+1=0的一个根,则m的值是( )
| A. | 1 | B. | -1 | C. | 0 | D. | 2 |
2.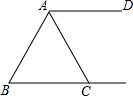 如图,AD∥BC,AC=BC,∠B=65°,则∠DAC的度数为( )
如图,AD∥BC,AC=BC,∠B=65°,则∠DAC的度数为( )
 如图,AD∥BC,AC=BC,∠B=65°,则∠DAC的度数为( )
如图,AD∥BC,AC=BC,∠B=65°,则∠DAC的度数为( )| A. | 50° | B. | 25° | C. | 60° | D. | 65° |
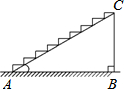 如图所示:是一段楼梯,高BC是5m,斜边AC是13m,如果在楼梯上铺地毯,那么至少需要地毯17米.
如图所示:是一段楼梯,高BC是5m,斜边AC是13m,如果在楼梯上铺地毯,那么至少需要地毯17米.