题目内容
如图,把梯形OBCD放在平面直角坐标系中,O为坐标原点,OB在x轴正半轴上,OB=5,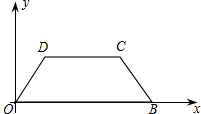 OD=BC=2,CD=3.
OD=BC=2,CD=3.(1)直接写出∠DOB的度数;
(2)一动点M从点O出发,沿O→B→C→D→O以每秒1个单位的速度运动,运动到点O停止.
①当点M在OB上运动时,若∠DMC=∠DOB,请求出此时点M的坐标;
②设点M的运动时间为t秒,当点M在B→C→D→O上运动时,过点M作MN⊥x轴,垂足为N,问:当t为何值时,△MNB的面积等于
| ||
| 4 |
分析:(1)从D点往OB作垂线DM,结合图形求出OM,根据直角三角形性质可得出∠DOB.
(2)先证∠1=∠2,再证△ODM∽△BMC,设OM=x,由相似比列出方程求解即可.
(3)分M点在DC,CB,BO上运动时三种情况作讨论.
当点M在BC上运动时,如图1,此时5<t≤7,用t表示BN,MN,然后用表示出△MNB的面积求解即可;
当点M在DO上运动时,如图3,此时7<t≤10,用t表示BN,MN,然后用表示出△MNB的面积求解即可;
当点M在DO上运动时,如图3,此时10<t≤12,用t表示BN,MN,然后用表示出△MNB的面积求解即可.
(2)先证∠1=∠2,再证△ODM∽△BMC,设OM=x,由相似比列出方程求解即可.
(3)分M点在DC,CB,BO上运动时三种情况作讨论.
当点M在BC上运动时,如图1,此时5<t≤7,用t表示BN,MN,然后用表示出△MNB的面积求解即可;
当点M在DO上运动时,如图3,此时7<t≤10,用t表示BN,MN,然后用表示出△MNB的面积求解即可;
当点M在DO上运动时,如图3,此时10<t≤12,用t表示BN,MN,然后用表示出△MNB的面积求解即可.
解答: 解:(1)如图,从D点往OB坐垂线DM,由图形可得OM=1,根据直角三角形性质可得出∠1=30°
解:(1)如图,从D点往OB坐垂线DM,由图形可得OM=1,根据直角三角形性质可得出∠1=30°
∴∠DOB=60°.(3分)
(2)①如图,∵∠DMC=∠DOB=60°,
∴∠1+∠3=120°,∠2+∠3=120°,
∴∠1=∠2(4分)
又∵∠DOM=∠MBC=60°
∴△ODM∽△BMC(5分)
∴
=
设OM=x,则2×2=x(5-x),解得x=1或4(6分)
∴M(1,0)或(4,0);(7分)
②(I)当点M在BC上运动时,如图1,此时5<t≤7,
∵MB=t-5
BN=
(t-5),MN=
(t-5)(8分)
∴S△MNB=
•
(t-5)•
(t-5)=
,
解得t1=5+
,t2=5-
(不合,舍去)(9分)
(II)当点M在CD上运动时,如图2,此时7<t≤10,
可求得BN=(t-7)+1=t-6,MN=
(10分)
∴S△MNB=
•(t-6)•
=
解得t=6.5(不合,舍去)(11分)
(III)当点M在DO上运动时,如图3,此时10<t≤12,
∵OM=12-t,ON=
(12-t),MN=
(12-t),
∴BN=OB-ON=5-
(12-t)=
(12分)
∴S△MNB=
•
•
(12-t)=
解得t1=7+
,t2=7-
(不合,舍去)(13分)
综合(I)(II)(III)可知,当t=5+
或t=7+
时,S△MNB=
.

 解:(1)如图,从D点往OB坐垂线DM,由图形可得OM=1,根据直角三角形性质可得出∠1=30°
解:(1)如图,从D点往OB坐垂线DM,由图形可得OM=1,根据直角三角形性质可得出∠1=30°∴∠DOB=60°.(3分)
(2)①如图,∵∠DMC=∠DOB=60°,
∴∠1+∠3=120°,∠2+∠3=120°,
∴∠1=∠2(4分)
又∵∠DOM=∠MBC=60°
∴△ODM∽△BMC(5分)
∴
| OD |
| BM |
| OM |
| BC |
设OM=x,则2×2=x(5-x),解得x=1或4(6分)
∴M(1,0)或(4,0);(7分)
②(I)当点M在BC上运动时,如图1,此时5<t≤7,
∵MB=t-5
BN=
| 1 |
| 2 |
| ||
| 2 |
∴S△MNB=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
解得t1=5+
| 2 |
| 2 |
(II)当点M在CD上运动时,如图2,此时7<t≤10,
可求得BN=(t-7)+1=t-6,MN=
| 3 |
∴S△MNB=
| 1 |
| 2 |
| 3 |
| ||
| 4 |
解得t=6.5(不合,舍去)(11分)
(III)当点M在DO上运动时,如图3,此时10<t≤12,
∵OM=12-t,ON=
| 1 |
| 2 |
| ||
| 2 |
∴BN=OB-ON=5-
| 1 |
| 2 |
| t-2 |
| 2 |
∴S△MNB=
| 1 |
| 2 |
| t-2 |
| 2 |
| ||
| 2 |
| ||
| 4 |
解得t1=7+
| 23 |
| 23 |
综合(I)(II)(III)可知,当t=5+
| 2 |
| 23 |
| ||
| 4 |

点评:本题涉及梯形及相似三角形的相关性质,难度中上.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
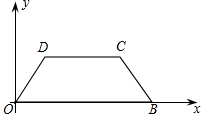 OD=BC=2,CD=3.
OD=BC=2,CD=3. ?
? ?
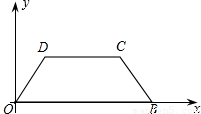
?
 ?
?