题目内容
在平面直角坐标系中，点A坐标为（3，4），P是x轴上一点，若△AOP是以OA为腰的等腰三角形，则点P的坐标为考点：等腰三角形的判定,坐标与图形性质
专题：
分析：本题应先求出OA的长，再分别讨论OA=OP、AP=OA、AP=OP的各种情况，即可得出答案．
解答：解：如图，
OA=
=5；
①若OA=AP，则点P1（6，0）；
②若OA=OP，则点P2（5，0），P3（-5，0）；
∴符合条件的P点的坐标为：（6，0），（5，0），（-5，0）．
故答案为：（6，0），（5，0），（-5，0）．
OA=
| 32+42 |
①若OA=AP，则点P1（6，0）；
②若OA=OP，则点P2（5，0），P3（-5，0）；
∴符合条件的P点的坐标为：（6，0），（5，0），（-5，0）．
故答案为：（6，0），（5，0），（-5，0）．
点评：本题考查了等腰三角形的性质及坐标与图形性质，难度适中，关键是掌握△AOP为等腰三角形时，那么任意一对邻边可为等腰三角形，注意分情况讨论．
练习册系列答案
相关题目
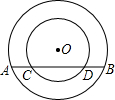如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C、D两点，设大圆和小圆的半径分别为a、b，求证：AD•BD=a2-b2．
如图所示，李华同学在在直角坐标系中画了反比例函数y=