Question

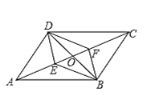
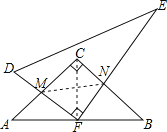
【题目】一副三角板如图摆放，点F是 45°角三角板△ABC的斜边的中点，AC＝4．当 30°角三角板DEF的直角顶点绕着点F旋转时，直角边DF，EF分别与AC，BC相交于点 M， N．在旋转过程中有以下结论：①MF＝NF；②CF与MN可能相等吗；③MN 长度的最小值为 2；④四边形CMFN的面积保持不变； ⑤△CMN面积的最大值为 2．其中正确的个数是_________.（填写序号）.

Answer 1

【答案】①②④⑤

【解析】

利用两直角三角形的特殊角、性质及旋转的性质分别判断每一个结论，找到正确的即可．

解：①连接CF，

∵F为AB中点，AC=BC，∠ACB=90°，

∴AF=BF=CF，CF⊥AB，

∴∠AFM+∠CFM=90°．

∵∠DFE=90°，∠CFM+∠CFN=90°，

∴∠AFM=∠CFN．

同理，∵∠A+∠MCF=90°，∠MCF+∠FCN=90°，

∴∠A=∠FCN，

在△AMF与△CNF中，

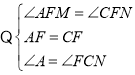
∴△AMF≌△CNF（ASA），

∴MF=NF．

故①正确；

∴②∵F是AB中点，△ABC是等腰直角三角形，
,

当M，N分别是AC，BC中点时，,

CF=MN，故正确；

③连接MN，当M为AC的中点时，CM=CN，根据边长为4知CM=CN=2，此时MN最小，最小值为，故③错误；

④当M、N分别为AC、BC中点时，四边形CMFN是正方形．

∵△AMF≌△CNF，

∴S△AMF=S△CNF

∴S四边形CDFE=S△AFC．

故④正确；

⑤由于△MNF是等腰直角三角形，因此当FM最小时，FN也最小；

即当DF⊥AC时，FM最小，此时，

，

当△CMN面积最大时，此时△FMN的面积最小．

此时S△CMN=S四边形CMFN-S△FMN=S△AFC-S△FMN=4-2=2，

故⑤正确．