题目内容
如图,在六边形ABCDEF中,AF∥CD,AB∥DE,BC∥EF,∠C=∠D=135°,则∠A的度数为________.
135°
分析:延长BC、ED交于G,根据已知求出∠G=90°,再根据平行线的性质即可求解.
解答: 解:135°.
解:135°.
如图,延长BC、ED交于G,
则∠GCD=180°-∠BCD=180°-135°=45°,
∠GDC=180°-∠CDE=180°-135°=45°,
∴∠G=180°-(∠GCD+∠GDC)
=180°-(45°+45°)
=90°,
∵AB∥ED,
∴∠B+∠G=180°,
∴∠B=90°,
又∵AF∥CD,
∴∠A+∠B+∠BCD=360°,
∴∠A+90°+135°=360°,
∴∠A=135°.
点评:考查了多边形内角与外角和平行线的性质,本题作辅助线是关键,学生一定要掌握作辅助线的能力.
分析:延长BC、ED交于G,根据已知求出∠G=90°,再根据平行线的性质即可求解.
解答:
 解:135°.
解:135°.如图,延长BC、ED交于G,
则∠GCD=180°-∠BCD=180°-135°=45°,
∠GDC=180°-∠CDE=180°-135°=45°,
∴∠G=180°-(∠GCD+∠GDC)
=180°-(45°+45°)
=90°,
∵AB∥ED,
∴∠B+∠G=180°,
∴∠B=90°,
又∵AF∥CD,
∴∠A+∠B+∠BCD=360°,
∴∠A+90°+135°=360°,
∴∠A=135°.
点评:考查了多边形内角与外角和平行线的性质,本题作辅助线是关键,学生一定要掌握作辅助线的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
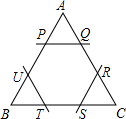 如图所示,△ABC是边长为a的正三角形纸张,今在各角剪去一个三角形,使得剩下的六边形PQRSTU为正六边形,则此正六边形的周长为何( )
如图所示,△ABC是边长为a的正三角形纸张,今在各角剪去一个三角形,使得剩下的六边形PQRSTU为正六边形,则此正六边形的周长为何( )| A、2a | ||
| B、3a | ||
C、
| ||
D、
|
 23、如图,在六边形ABCDEF中,AB=BC=CD=DE=EF=FA,∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,对角线AE与BF相交于点M,BD与CE相交于点N.
23、如图,在六边形ABCDEF中,AB=BC=CD=DE=EF=FA,∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,对角线AE与BF相交于点M,BD与CE相交于点N.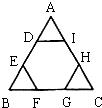 18、如图,正六边形DEFGHI的顶点都在边长为6cm的正三角形ABC的边上,则这个正六边形的边长是
18、如图,正六边形DEFGHI的顶点都在边长为6cm的正三角形ABC的边上,则这个正六边形的边长是 如图,在六边形ABCDEF中,BA⊥FA,BC⊥DC,∠α、∠β分别是∠ABC和∠EDC的补角,∠α=55°,∠β=30°,则∠E+∠F的度数为
如图,在六边形ABCDEF中,BA⊥FA,BC⊥DC,∠α、∠β分别是∠ABC和∠EDC的补角,∠α=55°,∠β=30°,则∠E+∠F的度数为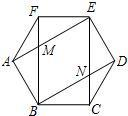 如图,在六边形ABCDEF中,AB=BC=CD=DE=EF=FA,∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,对角线AE与BF相交于点M,BD与CE相交于点N.
如图,在六边形ABCDEF中,AB=BC=CD=DE=EF=FA,∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,对角线AE与BF相交于点M,BD与CE相交于点N.