题目内容
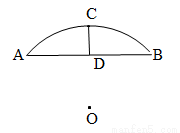
如图,某座桥的桥拱是圆弧形,它的跨度AB为8米,拱高CD为2米,求桥拱的半径.
5.
【解析】
试题分析:设圆的半径为R米,由于CD平分弧AB,且CD⊥AB,根据垂径定理的推论得到圆心O在CD的延长线上,再根据垂径定理得到CD平分AB,则AD= AB=4,在Rt△OAD中,利用勾股定理可计算出半径R.
AB=4,在Rt△OAD中,利用勾股定理可计算出半径R.
试题解析:如图,设圆的半径为R米,连OA,
∵CD平分弧AB,且CD⊥AB,∴圆心O在CD的延长线上,∴CD平分AB,∴AD= AB=4,
AB=4,
在Rt△OAD中,AD=4,OA=R,OD=R﹣CD=R﹣2,
∵ ,
,
∴ ,
,
解得R=5,
即拱桥所在圆的半径5米.

考点:1.垂径定理的应用;2.勾股定理.

练习册系列答案
相关题目

 与
与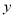 轴交于点C,与
轴交于点C,与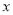 轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.

 ③;(2)①③
③;(2)①③ ②;(3)②③
②;(3)②③