题目内容
 24、已知命题:“如图,点A、D、B、E在同一条直线上,且AD=BE,AC∥DF,则△ABC≌△DEF.”这个命题是真命题还是假命题?如果是真命题,请给出证明; 如果是假命题,请添加一个适当的条件,使它成为真命题,并加以证明.
24、已知命题:“如图,点A、D、B、E在同一条直线上,且AD=BE,AC∥DF,则△ABC≌△DEF.”这个命题是真命题还是假命题?如果是真命题,请给出证明; 如果是假命题,请添加一个适当的条件,使它成为真命题,并加以证明.分析:因为AC∥DF,所以可得∠CAB=∠FDE.又AD=BE,若使△ABC≌△DEF,则缺少的条件可以是一对角或一对边,所以添加AC=DF问题可得证.
解答:这个命题是假命题.若AC=DF,则原命题是真命题.
证明:∵AD=BE,
∴AD+BD=BE+BD.
∴AB=DE.
∵AC∥DF,
∴∠CAB=∠FDE.
又∵AC=DF,
∴△ABC≌△DEF.
证明:∵AD=BE,
∴AD+BD=BE+BD.
∴AB=DE.
∵AC∥DF,
∴∠CAB=∠FDE.
又∵AC=DF,
∴△ABC≌△DEF.
点评:本题考查了全等三角形的判断,常用的判断方法为:SAS,SSS,AAS,ASA.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
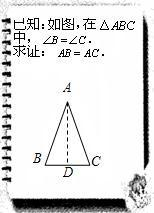
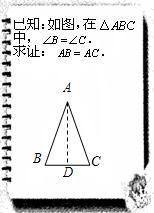 24、文文和彬彬在证明“有两个角相等的三角形是等腰三角形”这一命题时,画出图形,写出“已知”,“求证”(如图),她们对各自所作的辅助线描述如下:
24、文文和彬彬在证明“有两个角相等的三角形是等腰三角形”这一命题时,画出图形,写出“已知”,“求证”(如图),她们对各自所作的辅助线描述如下: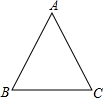
 作
作 的中垂线
的中垂线 ,垂足为
,垂足为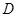 ”;
”; 的角平分线
的角平分线
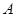 作
作 的中垂线
的中垂线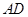 ,垂足为
,垂足为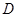 ”;
”;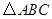 的角平分线
的角平分线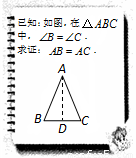
 要订正.”
要订正.”