��Ŀ����
��ͼ��������y=ax2+bx+c��a��0����y�ύ�ڵ�C��0��4������x�ύ�ڵ�A�͵�B�����е�A������Ϊ����2��0���������ߵĶԳ���x=1�������߽��ڵ�D����ֱ��BC���ڵ�E��
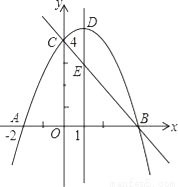
��1���������ߵĽ���ʽ��
��2����ֱ��BC�ĺ�������ʽΪy��=kx+b,������y<y��ʱ���Ա���x��ȡֵ��Χ.
��3��ƽ����DE��һ����ֱ��l��ֱ��BC�ཻ�ڵ�P�����������ཻ�ڵ�Q������D��E��P��QΪ������ı�����ƽ���ı��Σ����P�����꣮
��1��y=-x2+x+4����2��x<0 ��x>4����3��P1��3��1����P2���� ����P3�� �� ��. �������������������1���Ȱ�C��0��4������y=ax2+bx+c���ó�c=4�٣����������ߵĶԳ���x=-=1���õ�b=-2a�ڣ������߹���A��-2��0�����õ�0=4a-2b+c�ۣ�Ȼ���ɢ٢ڢۿɽ�ã�a=-��b=1��c=4��������������ߵĽ���ʽΪy=-x2+x+4�� ��2���������...
��ϰ��ϵ�д�
 Сѧ������ҵϵ�д�
Сѧ������ҵϵ�д� ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�
�����Ŀ


 B.
B. 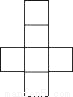 C.
C.  D.
D. 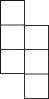
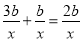 B.
B. 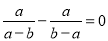 C.
C.  D.
D.