题目内容
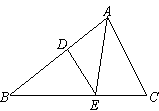
如图所示，O为△ABC的外心，若∠BAC=70°，则∠OBC=20°
20°
．分析：首先连接OC，由O为△ABC的外心，∠BAC=70°，根据圆周角定理，即可求得∠BOC的度数，又由OB=OC，根据等腰三角形的性质与三角形内角和定理，即可求得∠OBC的度数．
解答：
解：连接OC，
∵∠BAC=70°，
∴∠BOC=2∠BAC=140°，
∵OB=OC，
∴∠OBC=∠OCB=
=20°．
故答案为：20°．
解：连接OC，∵∠BAC=70°，
∴∠BOC=2∠BAC=140°，
∵OB=OC，
∴∠OBC=∠OCB=
| 180°-∠BOC |
| 2 |
故答案为：20°．
点评：此题考查了圆周角定理、等腰三角形的性质以及三角形内角和定理．此题难度不大，解题的关键是注意掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半定理的应用．
练习册系列答案
相关题目
2、如图所示，D为AB边上一点，AD：DB=3：4，DE∥AC交BC于点E，则S△BDE：S△AEC等于（ ）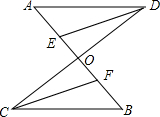
已知如图所示，O为AB、CD的中点，AE=BF，你从图中可以找到全等三角形共（ ）
