题目内容
关于x的不等式(2a-b)x-3a+2b>0的解集是x< ,则不等式ax+b>0的解集是________.
,则不等式ax+b>0的解集是________.
x<-
分析:由已知不等式及解集的特点,得到2a-b<0,移项并把x系数化为1后,根据解集得到关于a与b的关系,整理后得到a=2b,代入2a-b<0中,得到b<0,然后把a=2b代入所求的不等式中,两边同时除以b,不等号方向改变,得到关于x的不等式,求出不等式的解集即可.
解答:(2a-b)x-3a+2b>0,
移项得:(2a-b)x>3a-2b,
由已知解集为x< ,得到2a-b<0,
,得到2a-b<0,
变形得:x<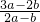 ,
,
可得: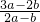 =
= ,整理得:a=2b,
,整理得:a=2b,
∴2a-b=4b-b=3b<0,即b<0,
∴不等式ax+b>0可化为2bx+b>0,
两边同时除以b得:2x+1<0,
解得:x<- ,
,
则不等式ax+b>0的解集是x<- .
.
故答案为:x<- .
.
点评:此题考查了一元一次不等式的解法,利用了转化及代入的数学思想,熟练掌握不等式的基本性质2(在不等式两边同时乘(除)以同一个负数时,不等号方向改变)是解本题的关键.

分析:由已知不等式及解集的特点,得到2a-b<0,移项并把x系数化为1后,根据解集得到关于a与b的关系,整理后得到a=2b,代入2a-b<0中,得到b<0,然后把a=2b代入所求的不等式中,两边同时除以b,不等号方向改变,得到关于x的不等式,求出不等式的解集即可.
解答:(2a-b)x-3a+2b>0,
移项得:(2a-b)x>3a-2b,
由已知解集为x<
 ,得到2a-b<0,
,得到2a-b<0,变形得:x<
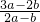 ,
,可得:
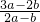 =
= ,整理得:a=2b,
,整理得:a=2b,∴2a-b=4b-b=3b<0,即b<0,
∴不等式ax+b>0可化为2bx+b>0,
两边同时除以b得:2x+1<0,
解得:x<-
 ,
,则不等式ax+b>0的解集是x<-
 .
.故答案为:x<-
 .
.点评:此题考查了一元一次不等式的解法,利用了转化及代入的数学思想,熟练掌握不等式的基本性质2(在不等式两边同时乘(除)以同一个负数时,不等号方向改变)是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果关于x的不等式(2a-1)x>2a-1的解集为x<1,那么a的取值范围是( )
A、a>
| ||
B、a<
| ||
C、a>-
| ||
D、a<-
|
 关于x的不等式3x-2a≤-2的解集如图所示,则a的值是
关于x的不等式3x-2a≤-2的解集如图所示,则a的值是