题目内容
未知数x,y满足(x2+y2)m2-2y(x+n)m+y2+n2=0,其中m,n表示非零已知数.求x,y的值.
解:将已知等式变形为:
m2x2+m2y2-2mxy-2mny+y2+n2=0,
(m2x2-2mxy+y2)+(m2y2-2mny+n2)=0,
即(mx-y)2+(my-n)2=0.
∴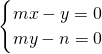 ,
,
∵m≠0,
∴y= ,x=
,x= .
.
分析:由原等式含有两个未知数,一个方程,对方程左边的代数式进行恒等变形,经过配方之后,化成几个非负数和为零的形式即可求解.
点评:本题考查了配方法的应用,难度适中,关键是掌握几个非负数和为零则这几个数分别为0.
m2x2+m2y2-2mxy-2mny+y2+n2=0,
(m2x2-2mxy+y2)+(m2y2-2mny+n2)=0,
即(mx-y)2+(my-n)2=0.
∴
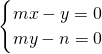 ,
,∵m≠0,
∴y=
 ,x=
,x= .
.分析:由原等式含有两个未知数,一个方程,对方程左边的代数式进行恒等变形,经过配方之后,化成几个非负数和为零的形式即可求解.
点评:本题考查了配方法的应用,难度适中,关键是掌握几个非负数和为零则这几个数分别为0.

练习册系列答案
相关题目