题目内容
已知关于x的方程kx2-2(k+1)x-1=0有两个不相等实数根,求k的取值范围.
考点:根的判别式,一元二次方程的定义
专题:
分析:先根据一元二次方程有两个不相等实数根列出关于k的不等式组,求出k的取值范围即可.
解答:解:∵关于x的方程kx2-2(k+1)x-1=0有两个不相等实数根,
∴
,即△=[-2(k+1)]2+4k>0且k≠0,解得k>
且k≠0或k<
.
∴
|
-3+
| ||
| 2 |
-3-
| ||
| 2 |
点评:本题考查的是根的判别式及一元二次方程的定义,熟知一元二次方程ax2+bx+c=0(a≠0)的根与△的关系是解答此题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
下列等式中,从左边到右边的变形为分解因式的是( )
| A、12a2b=3a•4ab |
| B、(x+2)(x-2)=x2-4 |
| C、4x2-8x-1=4x(x-2)-1 |
| D、2ax-2ay=2a(x-y) |
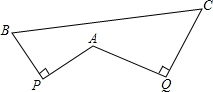 如图,PA=PB且PA⊥PB,QA=QC且QA⊥QC.
如图,PA=PB且PA⊥PB,QA=QC且QA⊥QC. 如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,AD=2,BC=BD=3,AC=4.
如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,AD=2,BC=BD=3,AC=4.