题目内容
已知x,y均为实数,且满足关系式x2-2x-6=0,y2-2y-6=0,则 =________.
=________.
- 或2
或2
分析:当x=y时,容易求解;
当x≠y时,由关系式x2-2x-6=0,y2-2y-6=0,可知x、y是z2-2z-6=0的两根,由根与系数的关系,求出x+y与xy的值,再根据 =
= ,代入即可求值.
,代入即可求值.
解答:当x≠y时,
∵x、y满足关系式x2-2x-6=0,y2-2y-6=0,
∴x、y是z2-2z-6=0的两根,
∴x+y=2,xy=-6,
∴ =
= =
=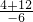 =-
=- .
.
当x,y的值相等时,原式=2.
故答案为:- 或2.
或2.
点评:本题容易忽视的情况是x,y可能是同一个值这一个情况.
 或2
或2分析:当x=y时,容易求解;
当x≠y时,由关系式x2-2x-6=0,y2-2y-6=0,可知x、y是z2-2z-6=0的两根,由根与系数的关系,求出x+y与xy的值,再根据
 =
= ,代入即可求值.
,代入即可求值.解答:当x≠y时,
∵x、y满足关系式x2-2x-6=0,y2-2y-6=0,
∴x、y是z2-2z-6=0的两根,
∴x+y=2,xy=-6,
∴
 =
= =
=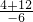 =-
=- .
.当x,y的值相等时,原式=2.
故答案为:-
 或2.
或2.点评:本题容易忽视的情况是x,y可能是同一个值这一个情况.

练习册系列答案
相关题目
