题目内容
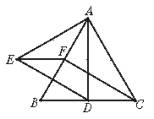
 25、已知:如图AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,求证:BE⊥AC.
25、已知:如图AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,求证:BE⊥AC.分析:由题中条件可得Rt△BDF≌Rt△ADC,得出对应角相等,再通过角之间的转化,进而可得出结论.
解答:证明:∵BF=AC,FD=CD,AD⊥BC,
∴Rt△BDF≌Rt△ADC(HL)
∴∠C=∠BFD,
∵∠DBF+∠BFD=90°,
∴∠C+∠DBF=90°,
∵∠C+∠DBF+∠BEC=180°
∴∠BEC=90°,即BE⊥AC.
∴Rt△BDF≌Rt△ADC(HL)
∴∠C=∠BFD,
∵∠DBF+∠BFD=90°,
∴∠C+∠DBF=90°,
∵∠C+∠DBF+∠BEC=180°
∴∠BEC=90°,即BE⊥AC.
点评:本题主要考查了全等三角形的判定及性质,能够熟练运用其性质求解一些简单的计算、证明问题.

练习册系列答案
相关题目
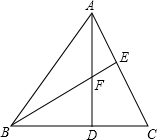 已知:如图AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,求证:BE⊥AC.
已知:如图AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,求证:BE⊥AC.
