Question

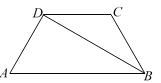
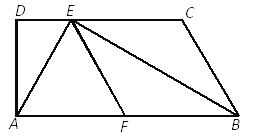
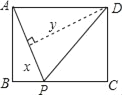
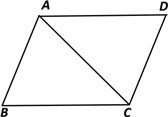
【题目】如图，已知平行四边形ABCD中，AC=BC，∠ACB=45°，将三角形ABC沿着AC翻折，点B落在点E处，联结DE，那么的值为________．

Answer 1

【答案】

【解析】分析：依据△ACF和△DEF都是等腰直角三角形，设EF=DF=1，则DE=，设AF=CF=x，则AC=EC=1+x．在Rt△ACF中，依据AF2+CF2=AC2，可得x2+x2=（x+1）2，解得x=1+，即可得到AC=2+，进而得出==．

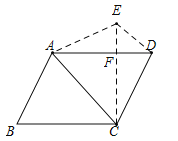
详解：如图，设AD与CE交于点F，由折叠可得，∠ACE=∠ACB=45°，而∠DAC=∠ACB=45°，∴∠AFC=90°，∠EFD=90°，AF=CF，由折叠可得，CE=AD，∴EF=DF，∴△ACF和△DEF都是等腰直角三角形，设EF=DF=1，则DE=，设AF=CF=x，则AC=EC=1+x．∵Rt△ACF中，AF2+CF2=AC2，∴x2+x2=（x+1）2，解得：x=1+或x=1﹣（舍去），∴AC=2+==．

故答案为：．