题目内容
 如图,一根长6
如图,一根长6 米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,与地面的倾斜角(∠ABO)为60°.当木棒A端沿墙下滑至点A′时,B端沿地面向右滑行至点B′.
米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,与地面的倾斜角(∠ABO)为60°.当木棒A端沿墙下滑至点A′时,B端沿地面向右滑行至点B′.
(1)求OB的长;
(2)当AA′=1米时,求BB′的长.
解:(1)根据题意可知:AB=6 ,∠ABO=60°,∠AOB=90°,
,∠ABO=60°,∠AOB=90°,
在Rt△AOB中,∵cos∠ABO= ,
,
∴OB=ABcos∠ABO=6 cos60°=3
cos60°=3 米,
米,
∴OB的长为3 米;
米;
(2)根据题意可知A′B′=AB=6 米,
米,
在Rt△AOB中,∵sin∠ABO=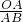 ,
,
∴OA=ABsin∠ABO=6 sin60°=9米,
sin60°=9米,
∵OA′=OA-AA′,AA′=1米,
∴OA′=8米,
在Rt△A′OB′中,OB′=2 米,
米,
∴BB′=OB′-OB=(2 -3
-3 )米.
)米.
分析:(1)由已知数据解直角三角形AOB即可;
(2)首先求出OA的长和OA′的长,再根据勾股定理求出OB′的长即可.
点评:本题考查了勾股定理的应用和特殊角的锐角三角函数,是中考常见题型.
 ,∠ABO=60°,∠AOB=90°,
,∠ABO=60°,∠AOB=90°,在Rt△AOB中,∵cos∠ABO=
 ,
,∴OB=ABcos∠ABO=6
 cos60°=3
cos60°=3 米,
米,∴OB的长为3
 米;
米;(2)根据题意可知A′B′=AB=6
 米,
米,在Rt△AOB中,∵sin∠ABO=
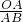 ,
,∴OA=ABsin∠ABO=6
 sin60°=9米,
sin60°=9米,∵OA′=OA-AA′,AA′=1米,
∴OA′=8米,
在Rt△A′OB′中,OB′=2
 米,
米,∴BB′=OB′-OB=(2
 -3
-3 )米.
)米.分析:(1)由已知数据解直角三角形AOB即可;
(2)首先求出OA的长和OA′的长,再根据勾股定理求出OB′的长即可.
点评:本题考查了勾股定理的应用和特殊角的锐角三角函数,是中考常见题型.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
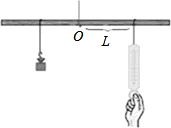 如图,取一根长1米长的匀质木杆,用细绳绑在木杆的中点O处并将其吊起来,在中点的左侧距离中点25cm处挂一个重9.8牛顿的物体,在中点右侧用一个弹簧秤向下拉,改变弹簧称与中点O的距离L(单位:cm),看弹簧秤的示数F(单位:牛顿)有什么变化,小明在做此《数学活动》时,得到下表的数据:
如图,取一根长1米长的匀质木杆,用细绳绑在木杆的中点O处并将其吊起来,在中点的左侧距离中点25cm处挂一个重9.8牛顿的物体,在中点右侧用一个弹簧秤向下拉,改变弹簧称与中点O的距离L(单位:cm),看弹簧秤的示数F(单位:牛顿)有什么变化,小明在做此《数学活动》时,得到下表的数据:| L/cm | 1 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| F/牛顿 | 125 | 24.5 | 16.5 | 12.3 | 9.8 | 8.2 | 7 | █ | 5.4 |
(1)当L=
(2)被墨水涂黑了的数据你认为大概是
(3)你能求出F与L的函数关系式吗?
(4)请你在直角坐标系中画出此函数的图象.
 如图所示,AC是一根垂直于地面的木杆,B是木杆上的一点,且AB=2米,D是地面上一点,AD=3米.在B处有甲、乙两只猴子,D处有一堆食物.甲猴由B往下爬到A处再从地面直奔D处,乙猴则向上爬到木杆顶C处腾空直扑到D处,如果两猴所经过的距离相等,则木杆的长为( )
如图所示,AC是一根垂直于地面的木杆,B是木杆上的一点,且AB=2米,D是地面上一点,AD=3米.在B处有甲、乙两只猴子,D处有一堆食物.甲猴由B往下爬到A处再从地面直奔D处,乙猴则向上爬到木杆顶C处腾空直扑到D处,如果两猴所经过的距离相等,则木杆的长为( )A、
| ||
B、2
| ||
C、3
| ||
| D、5m |
如图取一根长1.2米的匀质木杆,用细绳绑在木杆的中点O处并将其吊起来.
在左侧距离中点30cm处挂一个重10N的物体,为了保持木杆水平,在右侧用一个弹簧秤竖直向下拉.改变弹簧称与中点O的距离(单位:cm),看弹簧秤的示数F(单位:N)有什么变化,小锐在做此活动时,得到下表的数据:
| l/cm | … | 10 | 15 | 20 | 25 | b | … |
| F/N | … | 30 | 20 | a | 12 | 10 | … |
(2)求F与l的函数解析式;
(3)在平面直角坐标系中画出此函数的图象.

 如图,取一根长1米长的匀质木杆,用细绳绑在木杆的中点O处并将其吊起来,在中点的左侧距离中点25cm处挂一个重9.8牛顿的物体,在中点右侧用一个弹簧秤向下拉,改变弹簧称与中点O的距离L(单位:cm),看弹簧秤的示数F(单位:牛顿)有什么变化,小明在做此《数学活动》时,得到下表的数据:
如图,取一根长1米长的匀质木杆,用细绳绑在木杆的中点O处并将其吊起来,在中点的左侧距离中点25cm处挂一个重9.8牛顿的物体,在中点右侧用一个弹簧秤向下拉,改变弹簧称与中点O的距离L(单位:cm),看弹簧秤的示数F(单位:牛顿)有什么变化,小明在做此《数学活动》时,得到下表的数据:
| L/cm | 1 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| F/牛顿 | 125 | 24.5 | 16.5 | 12.3 | 9.8 | 8.2 | 7 | █ | 5.4 |
(1)当L=______cm时的数据是错了;
(2)被墨水涂黑了的数据你认为大概是______;
(3)你能求出F与L的函数关系式吗?
(4)请你在直角坐标系中画出此函数的图象.
