题目内容
在平面直角坐标系中若一个圆分别与x轴、y轴相交于点(-2,0),(-4,0),(0,-1),则这个圆与y轴的另一个交点坐标是________.
(0,-8)
分析:根据题意可得点A的坐标为(-4,0)、点B的坐标为(-2,0)、点C的坐标为(0,-1),作O′D⊥AB于D点,O′E⊥CE于E点,连接O′B、O′C,得到BD=1,O′E=DO=3,OC=1,设CE=FE=x,然后用含x的式子表示O′D=EO=1+x,利用勾股定理求得x= ,进而求得FC=2EC=7,故圆与y轴的另一个交点F的坐标为(0,-8).
,进而求得FC=2EC=7,故圆与y轴的另一个交点F的坐标为(0,-8).
解答: 解:如图知点A的坐标为(-4,0)、点B的坐标为(-2,0)、点C的坐标为(0,-1),
解:如图知点A的坐标为(-4,0)、点B的坐标为(-2,0)、点C的坐标为(0,-1),
作O′D⊥AB于D点,O′E⊥CE于E点,连接O′B、O′C,
∴AD=BD,CE=FE,
∴BD=1,O′E=DO=3,OC=1,
设CE=FE=x,
则O′D=EO=1+x,
∵O′B=O′C,
∴ =
=
解得x= ,
,
∴FC=2EC=7,
∴圆与y轴的另一个交点F的坐标为(0,-8),
故答案为(0,-8).
点评:此题考查了垂径定理,以及勾股定理的应用.此题难度适中,解题的关键是数形结合思想的应用,注意辅助线的作法.
分析:根据题意可得点A的坐标为(-4,0)、点B的坐标为(-2,0)、点C的坐标为(0,-1),作O′D⊥AB于D点,O′E⊥CE于E点,连接O′B、O′C,得到BD=1,O′E=DO=3,OC=1,设CE=FE=x,然后用含x的式子表示O′D=EO=1+x,利用勾股定理求得x=
 ,进而求得FC=2EC=7,故圆与y轴的另一个交点F的坐标为(0,-8).
,进而求得FC=2EC=7,故圆与y轴的另一个交点F的坐标为(0,-8).解答:
 解:如图知点A的坐标为(-4,0)、点B的坐标为(-2,0)、点C的坐标为(0,-1),
解:如图知点A的坐标为(-4,0)、点B的坐标为(-2,0)、点C的坐标为(0,-1),作O′D⊥AB于D点,O′E⊥CE于E点,连接O′B、O′C,
∴AD=BD,CE=FE,
∴BD=1,O′E=DO=3,OC=1,
设CE=FE=x,
则O′D=EO=1+x,
∵O′B=O′C,
∴
 =
=
解得x=
 ,
,∴FC=2EC=7,
∴圆与y轴的另一个交点F的坐标为(0,-8),
故答案为(0,-8).
点评:此题考查了垂径定理,以及勾股定理的应用.此题难度适中,解题的关键是数形结合思想的应用,注意辅助线的作法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
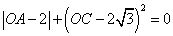 .
.