题目内容
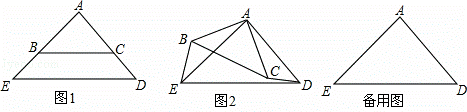
如图1,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上.
(1)请直接写出线段BE与线段CD的关系: ;
(2)如图2,将图1中的△ABC绕点A顺时针旋转角α(0<α<360°),
①(1)中的结论是否成立?若成立,请利用图2证明;若不成立,请说明理由;
②当AC= ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.
ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.
解:(1)∵△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,
∴AB=AC,AE=AD,
∴AE﹣AB=A D﹣AC,
D﹣AC,
∴BE=CD;
(2)①∵△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,
∴AB=AC,AE=AD,
由旋转的性质可得∠BAE=∠CAD,
在△BAE与△CAD中,
 ,
,
∴△BAE≌△CAD(SAS),
∴BE=CD;
②∵以A、B、C、D四点为顶点 的四边形是平行四边形,
的四边形是平行四边形,
∴∠ABC=∠ADC=45°,
∵AC= ED,
ED,
∴∠CAD=45°,
∴角α的度数是45°.

练习册系列答案
相关题目
 ×
× +
+ 的运算结果应在哪两个连续自然数之间( )
的运算结果应在哪两个连续自然数之间( )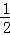 AD=4,求阴影部分的面积.
AD=4,求阴影部分的面积.

 我市质检部分对A、B、C、D四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出C厂家的合格率为95%,并根据检测数据绘制了如图1、图2两幅不完整的统计图.
我市质检部分对A、B、C、D四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出C厂家的合格率为95%,并根据检测数据绘制了如图1、图2两幅不完整的统计图.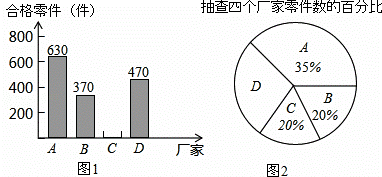
 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( ) B.
B. C.
C. D.
D.
 有意义,则实数x的取值范围是
有意义,则实数x的取值范围是 

