Question

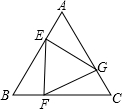（2013•天水）如图，已知等边三角形ABC的边长为2，E、F、G分别是边AB、BC、CA的点，且AE=BF=CG，设△EFG的面积为y，AE的长为x，则y与x的函数图象大致是（　　）

A．

B．

C．

D．

Answer 1

分析：根据题意可知△AEG≌△BEF≌△CFG三个三角形全等，且在△AEG中，AE=x，AG=2-x；可得△AEG的面积y与x的关系；进而可判断得则y关于x的函数的图象的大致形状．

解答：解：∵AE=BF=CG，且等边△ABC的边长为2，
∴BE=CF=AG=2-x；
∴△AEG≌△BEF≌△CFG．
在△AEG中，AE=x，AG=2-x，
∵S_△AEG=

1

2

AE×AG×sinA=

3

4

x（2-x）；
∴y=S_△ABC-3S_△AEG=

3

-3×

3

4

x（2-x）=

3

（

3

4

x²-

3

2

x+1）．
∴其图象为二次函数，且开口向上．
故选C．

点评：本题考查动点问题的函数图象，解答本题的关键是求出y与x的函数关系式，另外要求能根据函数解析式判断函数图象的形状．