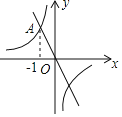Question

【题目】已知是关于的函数，若其函数图象经过点，则称点为函数图象上的“郡点”，例如：上存在“郡点”．

（1）直线___________（填写直线解析式）上的每一个点都是“郡点”，双曲线上的“郡点”是___________；

（2）若抛物线上有“郡点”，且“郡点”、（点和点可以重合）的坐标为、，求的最小值．

（3）若函数的图象上存在唯一的一个“郡点”，且当，的最小值，求的值．

Answer 1

【答案】（1）；或；（2）；（3）的值为或

【解析】

（1）根据“郡点”的定义得y＝x时，图象经过点P（t，t）；y＝＝x，函数图象经过点P（t，t），即可求解；

（2）由题意得：y＝x，即：y＝x2＋（a＋1）xa2a＋2＝x，整理得：

x2＋axa2a＋2＝0，由韦达定理，即可求解；

（3）由题意得：y＝x2＋（nk＋1）x＋m＋k1＝x，由题意△＝0得：m＝（nk）2（k1），分当2≤n＝k≤1、当n＝k≤2、n＝k≥1三种情况，求解即可．

解：（1）由题意得：y＝x时，图象经过点P（t，t），

y＝＝x，解得：x＝±1，

故答案为：y＝x，（1，1）或（1，1）；

（2）设二次函数的“郡点”为

∴

∴

∴

∴

又“郡点”、（点和点可以重合）

∴△≥0

∴

∴或

对于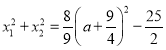

∵a=，对称轴a=-

∴时，

（3）∵只有一个“郡点”

∴与只有一个交点

=x

则方程有两个相同的根，

∴

可得

①当2≤n＝k≤1时，n＝k时，m取得最小值，

即：（k1）＝k，

解得：k＝；

②当n＝k≤2时，n＝2，m取得最小值，

即：（2k）2（k1）＝k，

x无解；

③当n＝k≥1时，n＝1，m取得最小值，

即：（1k）2span>（k1）＝k，

解得：k＝2±（舍去负值）

故：k的值为：或2＋．