题目内容
17.二次函数y=ax2+bx+c(a≠0)与x轴两交点坐标是(-1,0),(5,0),则关于x的一元二次方程ax2+bx+c=0的两根为x1=-1,x2=5.分析 根据抛物线与x轴的交点的横坐标是二次函数的函数值为0时所对应的自变量即即x=5或-1时,y=0,即可得到一元二次方程ax2+bx+c=0的两根.
解答 解:∵二次函数y=ax2+bx+c与x轴的交点坐标为(-1,0)、(5,0),即x=-1或5时,y=0,
∴一元二次方程ax2+bx+c=0的两根分别为:x1=-1,x2=5.
故答案为:x1=-1,x2=5.
点评 本题考查的是抛物线与x轴的交点问题,熟知交点的横坐标是二次函数的函数值为0时所对应的自变量,也考查了一元二次方程ax2+bx+c=0的根的含义.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
12.下列命题中,真命题是( )
| A. | 对角线相等的四边形是矩形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 两条对角线互相平分且相等的四边形是正方形 | |
| D. | 顺次连接四边形的各边中点所得的四边形是平行四边形 |
6.化简$\sqrt{8{a}^{2}}$的结果是( )
| A. | 4a$\sqrt{2}$ | B. | 16$\sqrt{{a}^{2}}$ | C. | 2a$\sqrt{4}$ | D. | 2a$\sqrt{2}$ |
7.用科学记数法表示0.000625,正确的是( )
| A. | 6.25×10-4 | B. | 625×10-6 | C. | 6.25×10-6 | D. | 0.625×10-3 |
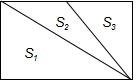 如图是由三个三角形组成的一个面积为(6a2+4a)cm2的长方形,三个三角形的面积分别是S1,S2,S3,若S1=(3a2+2a)cm2,S3=(2a2-a)cm2,则S2等于(a2+3a)cm2.
如图是由三个三角形组成的一个面积为(6a2+4a)cm2的长方形,三个三角形的面积分别是S1,S2,S3,若S1=(3a2+2a)cm2,S3=(2a2-a)cm2,则S2等于(a2+3a)cm2.
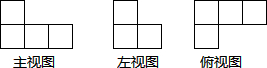 在一个仓库里堆放有若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画出来,如图,则这堆货箱共有5个.
在一个仓库里堆放有若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画出来,如图,则这堆货箱共有5个.