Question

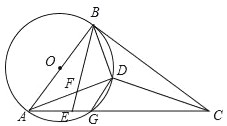
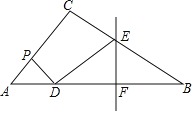
【题目】如图，在△ABC中，∠C=，点P在AC上运动，点D在AB上，PD始终保持与PA相等，BD的垂直平分线交BC于点E，交BD于点F，连接DE．若AC=6，BC=8，PA=2，则线段DE的长为________

Answer 1

【答案】

【解析】

连接OD，根据等腰三角形的性质得到∠A＝∠PDA，根据线段垂直平分线的性质得到EB＝ED，于是得到DE⊥DP；连接PE，设DE＝x，则EB＝ED＝x，CE＝8x，根据勾股定理即可得到结论．

∵PD＝PA，

∴∠A＝∠PDA，

∵EF是BD的垂直平分线，

∴EB＝ED，

∴∠B＝∠EDB，

∵∠C＝90°，

∴∠A＋∠B＝90°，

∴∠PDA＋∠EDB＝90°，

∴∠PDE＝180°90°＝90°，

∴DE⊥DP，

连接PE，

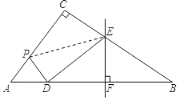
设DE＝x，则EB＝ED＝x，CE＝8x，

∵∠C＝∠PDE＝90°，

∴PC2＋CE2＝PE2＝PD2＋DE2，

∴42＋（8x）2＝22＋x2，

解得：x＝，

则DE＝．