Question

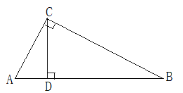
【题目】如图，在△ABC中，∠ACB=90°，CD是AB边上的高，AB=13cm，BC=12cm，AC=5cm．

（1）求△ABC的面积；

（2）求CD的长；

（3）作出△ABC的边AC上的中线BE，并求出△ABE的面积；

（4）作出△BCD的边BC上的高DF，当BD=时，试求出DF的长（用表示）．

Answer 1

【答案】（1）30；（2）；（3）图见解析，15；（4）图见解析，．

【解析】

（1）直接根据三角形面积公式加以计算即可；

（2）根据进一步计算即可；

（3）先根据题意画出边AC上的中线BE，然后根据三角形面积的与底边跟高的关系进一步求解即可；

（4）先根据题意作出图形，然后根据进一步求解即可.

（1）∵△ABC中，∠ACB=90°，BC=12cm，AC=5cm．

∴ ；

（2）∵CD是AB边上的高，

∴，

∴；

（3）

如图所示，BE是AC边上的中线，

∴AE=CE=，

∴；

（4）

如图所示，DF⊥BC，

∵

即：．．

∴．