题目内容
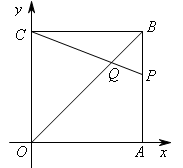
如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A,C分别在x,y轴的正半轴上.点Q在对角线OB上,且OQ=OC,连接CQ并延长CQ交边AB于点P,则点P的坐标为( , ).

 。
。试题分析:∵四边形OABC是边长为2的正方形,∴根据勾股定理,得对角线
 。
。∵OQ=OC,∴
 ,∠OCQ=∠OQC。
,∠OCQ=∠OQC。∵∠OCQ=∠BPQ(由平行可得),∠OQC=∠BQP(对顶角相等),∴∠BPQ=∠BQP。
∴
 。∴
。∴ 。
。又 ∵OA=2,∴点P的坐标为
 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 <0,点P(
<0,点P(
 )关于原点的对称点为
)关于原点的对称点为 ,则
,则 ,
, ,则P点的坐标是( )
,则P点的坐标是( )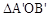 的位置,点B的横坐标为2,则点
的位置,点B的横坐标为2,则点 的坐标为
的坐标为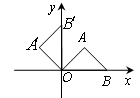
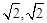 )
)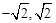 )
)