题目内容
 如图,已知∠AOB=α,在射线OA、OB上分别取点OA1=OB1,连接A1B1,在B1A1、B1B上分别取点A2、B2,使B1B2=B1A2,连接A2B2…按此规律继续下去,记∠A2B1B2=θ1,∠A3B2B3=θ2,…,∠An+1BnBn+1=θn则θ10=
如图,已知∠AOB=α,在射线OA、OB上分别取点OA1=OB1,连接A1B1,在B1A1、B1B上分别取点A2、B2,使B1B2=B1A2,连接A2B2…按此规律继续下去,记∠A2B1B2=θ1,∠A3B2B3=θ2,…,∠An+1BnBn+1=θn则θ10=
- A.

- B.

- C.

- D.

A
分析:设∠A1B1O=x,根据等腰三角形性质和三角形内角和定理得α+2x=180°,x=180°-θ1,即可求得θ1= ;同理求得θ2=
;同理求得θ2= ;即可发现其中的规律,按照此规律即可求得答案.
;即可发现其中的规律,按照此规律即可求得答案.
解答:设∠A1B1O=x,
则α+2x=180°,x=180°-θ1,
θ1= ;
;
设∠A2B2B1=y,
则θ2+y=180°①,
θ1+2y=180°②,
①×2-②得:2θ2-θ1=180°,
∴θ2= ;
;
…
θn= ;
;
则θ10= .
.
故选A.
点评:此题主要考查学生对等腰三角形性质和三角形内角和定理的理解和掌握,解答此题的关键是总结归纳出规律.
分析:设∠A1B1O=x,根据等腰三角形性质和三角形内角和定理得α+2x=180°,x=180°-θ1,即可求得θ1=
 ;同理求得θ2=
;同理求得θ2= ;即可发现其中的规律,按照此规律即可求得答案.
;即可发现其中的规律,按照此规律即可求得答案.解答:设∠A1B1O=x,
则α+2x=180°,x=180°-θ1,
θ1=
 ;
;设∠A2B2B1=y,
则θ2+y=180°①,
θ1+2y=180°②,
①×2-②得:2θ2-θ1=180°,
∴θ2=
 ;
;…
θn=
 ;
;则θ10=
 .
.故选A.
点评:此题主要考查学生对等腰三角形性质和三角形内角和定理的理解和掌握,解答此题的关键是总结归纳出规律.

练习册系列答案
相关题目
如图,已知∠AOB是直角,∠AOC是锐角,ON平分∠AOC,OM平分∠BOC,则∠MON是( )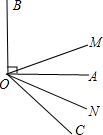

| A、45° | ||
B、45°+
| ||
C、60°-
| ||
| D、不能计算 |


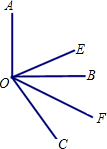 如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC.
如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC. 尺规作图:
尺规作图: 如图,已知∠AOB=x(0°<x<180°),OC平分∠AOB,点N为OB上一个定点.通过画图可以知道:当∠AOB=45°时,在射线OC上存在点P,使△ONP成为等腰三角形,且符合条件的点有三个,即P1(顶点为P2),P2(顶点为0),P3(顶点为N).
如图,已知∠AOB=x(0°<x<180°),OC平分∠AOB,点N为OB上一个定点.通过画图可以知道:当∠AOB=45°时,在射线OC上存在点P,使△ONP成为等腰三角形,且符合条件的点有三个,即P1(顶点为P2),P2(顶点为0),P3(顶点为N).