题目内容
(本题满分8分)如果规定“Φ”为一种新的运算: Φ
Φ .
.
例如: Φ
Φ ,请仿照例题计算:
,请仿照例题计算:
(1) Φ
Φ (2)
(2) Φ
Φ Φ
Φ
(1)-11; (2)-31
【解析】
试题分析:由题意可知Φ表示的运算法则是 Φ
Φ =
= ,由此法则可把特殊的运算转化为有理数的混合运算.
,由此法则可把特殊的运算转化为有理数的混合运算.
试题解析:(1)-2 Φ 3=-2×3+(-2) -
- =-11.
=-11.
(2)(-2)Φ [(-3)Φ 1 ]=(-2)Φ [-3×1+(-3) -1
-1 =(-2)Φ 5 =(-2)×5+(-2)
=(-2)Φ 5 =(-2)×5+(-2) -5
-5 =-31.
=-31.
考点:有理数的混合运算.
考点分析: 考点1:有理数 1、有理数的概念:正数和分数统称为有理数.2、有理数的分类:
①按整数、分数的关系分类; ②按正数、负数与0的关系分类.
有理数{整数{正整数0负整数分数{正分数负分数 有理数 {正数{正整数正分数0负数{负整数负分数
注意:如果一个数是小数,它是否属于有理数,就看它是否能化成分数的形式,所有的有限小数和无限循环小数都可以化成分数的形式,因而属于有理数,而无限不循环小数,不能化成分数形式,因而不属于有理数. 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
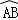 上的点D处,折痕交OA于点C,则
上的点D处,折痕交OA于点C,则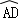 的长为 .
的长为 .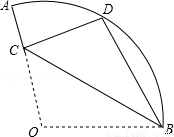

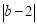 =0,则ab的值是( )
=0,则ab的值是( ) D.
D. ,
, ,
, (每两个2之间依次增加1个1),0,
(每两个2之间依次增加1个1),0, ,
, ,
,
 ,那么它们的和等于 .
,那么它们的和等于 .
 B、
B、 C、
C、 D、
D、