题目内容
 如图,在△ABC中,∠ABC=∠ACB=72°,BD平分∠ABC,图中共有
如图,在△ABC中,∠ABC=∠ACB=72°,BD平分∠ABC,图中共有考点:等腰三角形的判定与性质
专题:
分析:由∠ABC=∠ACB=72°可求得∠DBC=∠ABD=∠A=36°,故可判断出AB=AC,AD=BD,BD=BD,可得出等腰三角形的个数.
解答:解:∵∠ABC=∠ACB=72°,BD平分∠ABC,
∴∠A=∠ABD=∠DBC=36°,
∴∠BDC=∠BCD=72°,
∴AB=AC,DA=DB,BD=BC,
∴△ABC,△ABD,△BCD为等腰三角形,
故答案为:3.
∴∠A=∠ABD=∠DBC=36°,
∴∠BDC=∠BCD=72°,
∴AB=AC,DA=DB,BD=BC,
∴△ABC,△ABD,△BCD为等腰三角形,
故答案为:3.
点评:本题主要考查等腰三角形的判定,利用三角形内角和定理及角平分线得到角相等是解题的关键.

练习册系列答案
相关题目
以下列各组线段为边,能组成三角形的是( )
| A、2cm,3cm,5cm |
| B、3cm,3cm,6cm |
| C、5cm,8cm,2cm |
| D、4cm,5cm,6cm |
计算(x5)2的结果是( )
| A、x7 |
| B、x52 |
| C、x10 |
| D、x25 |
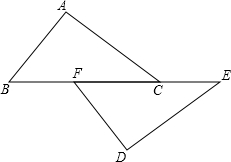 如图,点B、F、C、E在一条直线上,BC=EF,AB∥ED,AC∥FD,求证:AC=DF.
如图,点B、F、C、E在一条直线上,BC=EF,AB∥ED,AC∥FD,求证:AC=DF.