题目内容
 如图,A、B是双曲线
如图,A、B是双曲线  上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=12.则k=________.
上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=12.则k=________.
8
分析:分别过点A、B作x轴的垂线,垂足分别为D、E,再过点A作AF⊥BE于F,那么由AD∥BE,AD=2BE,可知B、E分别是AC、DC的中点,易证△ABF≌△CBE,则S△AOC=S梯形AOEF=12,根据梯形的面积公式即可求出k的值.
解答: 解:分别过点A、B作x轴的垂线,垂足分别为D、E,再过点A作AF⊥BE于F.
解:分别过点A、B作x轴的垂线,垂足分别为D、E,再过点A作AF⊥BE于F.
则AD∥BE,AD=2BE= ,
,
∴B、E分别是AC、DC的中点.
在△ABF与△CBE中,∠ABF=∠CBE,∠F=∠BEC=90°,AB=CB,
∴△ABF≌△CBE.
∴S△AOC=S梯形AOEF=12.
又∵A(a, ),B(2a,
),B(2a, ),
),
∴S梯形AOEF= (AF+OE)×EF=
(AF+OE)×EF= (a+2a)×
(a+2a)× =
=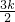 =12,
=12,
解得:k=8.
故答案为:8.
点评:本题主要考查了反比例函数的性质、三角形的中位线的判定及梯形的面积公式,体现了数形结合的思想,同学们要好好掌握.
分析:分别过点A、B作x轴的垂线,垂足分别为D、E,再过点A作AF⊥BE于F,那么由AD∥BE,AD=2BE,可知B、E分别是AC、DC的中点,易证△ABF≌△CBE,则S△AOC=S梯形AOEF=12,根据梯形的面积公式即可求出k的值.
解答:
 解:分别过点A、B作x轴的垂线,垂足分别为D、E,再过点A作AF⊥BE于F.
解:分别过点A、B作x轴的垂线,垂足分别为D、E,再过点A作AF⊥BE于F.则AD∥BE,AD=2BE=
 ,
,∴B、E分别是AC、DC的中点.
在△ABF与△CBE中,∠ABF=∠CBE,∠F=∠BEC=90°,AB=CB,
∴△ABF≌△CBE.
∴S△AOC=S梯形AOEF=12.
又∵A(a,
 ),B(2a,
),B(2a, ),
),∴S梯形AOEF=
 (AF+OE)×EF=
(AF+OE)×EF= (a+2a)×
(a+2a)× =
=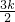 =12,
=12,解得:k=8.
故答案为:8.
点评:本题主要考查了反比例函数的性质、三角形的中位线的判定及梯形的面积公式,体现了数形结合的思想,同学们要好好掌握.

练习册系列答案
相关题目
 如图,A、B是双曲线
如图,A、B是双曲线 如图,C,D是双曲线y=
如图,C,D是双曲线y= 如图,A、B是双曲线 y=
如图,A、B是双曲线 y= (2011•沙县质检)如图,A、B两点是双曲线的一个分支上的两点,点B在点A右侧,并且B的坐标为(a,b),则a的取值范围是( )
(2011•沙县质检)如图,A、B两点是双曲线的一个分支上的两点,点B在点A右侧,并且B的坐标为(a,b),则a的取值范围是( )