题目内容
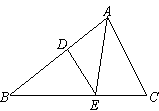
如图所示，E为□ABCD的边AD上的一点，且AE∶ED＝3∶2，CE交BD于F，则BF∶FD （ ）
A.3∶5 B.5∶3 C.2∶5 D.5∶2
【答案】
C.
【解析】
试题分析：由在▱ABCD中，且BE：EC=2：3，易得BE：AD=2：5，△ADF∽△EBF，然后根据相似三角形的对应边成比例，即可求得答案．
∵BE：EC=2：3，
∴BE：BC=2：5，
∵四边形ABCD是平行四边形，
∴AD=BC，AD∥BC，
∴BE：AD=2：5，△ADF∽△EBF，
∴
．
故选C.
考点: 1.相似三角形的判定与性质；2.平行四边形的性质．
练习册系列答案
相关题目
2、如图所示，D为AB边上一点，AD：DB=3：4，DE∥AC交BC于点E，则S△BDE：S△AEC等于（ ）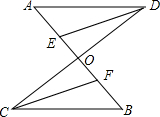
已知如图所示，O为AB、CD的中点，AE=BF，你从图中可以找到全等三角形共（ ）
