题目内容
 如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE.请证明△ABC≌△DEC.
如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE.请证明△ABC≌△DEC.考点:全等三角形的判定
专题:证明题
分析:根据同角的余角相等可得到∠3=∠5,结合条件可得到∠1=∠D,再加上BC=CE,可证得结论.
解答: 解:∵∠BCE=∠ACD=90°,
解:∵∠BCE=∠ACD=90°,
∴∠3+∠4=∠4+∠5,
∴∠3=∠5,
在△ACD中,∠ACD=90°,
∴∠2+∠D=90°,
∵∠BAE=∠1+∠2=90°,
∴∠1=∠D,
在△ABC和△DEC中,
,
∴△ABC≌△DEC(AAS).
 解:∵∠BCE=∠ACD=90°,
解:∵∠BCE=∠ACD=90°,∴∠3+∠4=∠4+∠5,
∴∠3=∠5,
在△ACD中,∠ACD=90°,
∴∠2+∠D=90°,
∵∠BAE=∠1+∠2=90°,
∴∠1=∠D,
在△ABC和△DEC中,
|
∴△ABC≌△DEC(AAS).
点评:本题主要考查全等三角形的判定,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
 如图,数轴上点P表示的数可能是( )
如图,数轴上点P表示的数可能是( )A、
| ||
B、
| ||
C、
| ||
D、
|
不解方程,一元二次方程3x2+2x+1=0的解的情况是( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、有一个实数根 |
| D、没有实数根 |
如果菱形的边长是2cm,一条对角线的长也是2cm,那么该菱形的另一条对角线的长是( )
| A、3cm | ||
| B、4cm | ||
C、
| ||
D、2
|
下列表述正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、无限小数都是无理数 |
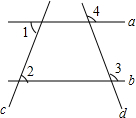 如图,已知:∠1=∠2,∠3=110°,求∠4的度数.
如图,已知:∠1=∠2,∠3=110°,求∠4的度数.