题目内容
2. 类比三角形中位线的定义,我们给出梯形中位线的定义:如图,在梯形ABCD中,AD∥BC,点E、F分别是AB、DC的中点,称线段EF为梯形ABCD的中位线.
类比三角形中位线的定义,我们给出梯形中位线的定义:如图,在梯形ABCD中,AD∥BC,点E、F分别是AB、DC的中点,称线段EF为梯形ABCD的中位线.(1)理解:如图,若点E是AB的中点,EF∥BC交CD于F,则EF是梯形ABCD的中位线吗?为什么?
(2)探究:如图,梯形ABCD的中位线EF与线段AD、BC三者之间的位置关系和数量关系如何?请说明理由:(点拨:可连接DE并延长交CB的延长线于G,这样就可把四边形的问题转化为三角形问题来解决)
(3)应用:如图,已知∠C=60°,CD=8,梯形中位线EF=6,求梯形ABCD的面积.
分析 (1)根据平行线等分线段定理证明即可;
(2)连接DE并延长交CB的延长线于H,证明△DAE≌△HBE,根据全等三角形的性质和三角形中位线定理解答即可;
(3)作DP⊥BC于P,根据正弦的定义求出DP,根据梯形中位线定理和梯形面积公式计算即可.
解答 解:(1)EF是梯形ABCD的中位线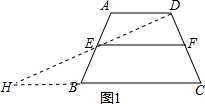 ,
,
∵AD∥BC,EF∥BC,
∴AD∥EF∥BC,
∴$\frac{AE}{EB}$=$\frac{DF}{FC}$,又点E是AB的中点,
∴点F是CD的中点,
∴EF是梯形ABCD的中位线;
(2)梯形的中位线平行于两底,并且等于两底和的一半.
如图1,连接DE并延长交CB的延长线于H,
∵AD∥BC,
∴∠DAE=∠HBE,
在△DAE和△HBE中,
$\left\{\begin{array}{l}{∠DAE=∠HBE}\\{AE=BE}\\{∠AED=∠BEH}\end{array}\right.$,
∴△DAE≌△HBE,
∴AD=BH,DE=EH,又点F是CD的中点,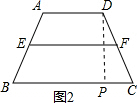
∴EF是△DHC的中位线,
∴EF∥BC,EF=$\frac{1}{2}$CH=$\frac{1}{2}$(AD+BC);
(3)如图2,作DP⊥BC于P,
sinC=$\frac{DP}{CD}$,
则DP=8×$\frac{\sqrt{3}}{2}$=4$\sqrt{3}$,
∵EF=$\frac{1}{2}$(AD+BC),
∴$\frac{1}{2}$(AD+BC)=6,
梯形ABCD的面积=$\frac{1}{2}$(AD+BC)×DP=24$\sqrt{3}$.
点评 本题考查的是梯形的中位线定理的推导和应用、全等三角形的判定和性质、平行线等分线段定理的应用,正确作出辅助线、构造全等三角形是解题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
12. 如图,已知∠ABC,小彬借助一把没有刻度且等宽的直尺,按如图的方法画出了∠ABC的平分线BP.他这样做的依据是( )
如图,已知∠ABC,小彬借助一把没有刻度且等宽的直尺,按如图的方法画出了∠ABC的平分线BP.他这样做的依据是( )
 如图,已知∠ABC,小彬借助一把没有刻度且等宽的直尺,按如图的方法画出了∠ABC的平分线BP.他这样做的依据是( )
如图,已知∠ABC,小彬借助一把没有刻度且等宽的直尺,按如图的方法画出了∠ABC的平分线BP.他这样做的依据是( )| A. | 在一个角的内部,且到角两边的距离相等的点在这个角的平分线上 | |
| B. | 角平分线上的点到这个角两边的距离相等 | |
| C. | 三角形三条角平分线的交点到三条边的距离相等 | |
| D. | 以上均不正确 |
 如图,在等腰△ABC中,AC=AB=17,BC=16,AD是BC边上的中线,BE⊥AC,交AC于点E,求BE的长.
如图,在等腰△ABC中,AC=AB=17,BC=16,AD是BC边上的中线,BE⊥AC,交AC于点E,求BE的长.