题目内容
7.若$\frac{a+b}{c}$=$\frac{b+c}{a}$=$\frac{a+c}{b}$=m,则关于x的一次函数y=mx+m必经过第( )象限.| A. | 一、二 | B. | 二、三 | C. | 三、四 | D. | 一、四 |
分析 分类讨论:当a+b+c=0,利用比例性质得M=-1,则函数解析式为y=-x-1,于是一次函数与系数的关系可得直线经过第二、三、四象限;当a+b+c≠0,利用比例性质得k=$\frac{2(a+b+c)}{a+b+c}$=2,则函数解析式为y=2x+2,于是一次函数与系数的关系可得直线经过第一、二、三象限,然后综合两种情况可判断y=kx-k的图象必经过第二、三象限.
解答 解:当a+b+c=0,m=-1,则函数解析式为y=-x-1,直线y=-x-1经过第二、三、四象限;
当a+b+c≠0,k=$\frac{a+b}{c}$=$\frac{b+c}{a}$=$\frac{a+c}{b}$=$\frac{2(a+b+c)}{a+b+c}$=2,则函数解析式为y=2x+2,直线y=2x+2经过第一、二、三象限,
所以关于x的函数y=mx+m的图象必经过第二、三象限.
故选B.
点评 本题考查了一次函数与系数的关系:由于y=kx+b与y轴交于(0,b),当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴.记住k>0,b>0?y=kx+b的图象在一、二、三象限;k>0,b<0?y=kx+b的图象在一、三、四象限;k<0,b>0?y=kx+b的图象在一、二、四象限;k<0,b<0?y=kx+b的图象在二、三、四象限.也考查了比例的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列说法中正确的是( )
| A. | $\sqrt{9}$等于±3 | |
| B. | 若点P(2,a)和点Q(b,-3)关于x轴对称,则a-b的值为1 | |
| C. | 函数$y=\frac{{\sqrt{x+1}}}{x}$的自变量的取值范围是x>-1且x≠0 | |
| D. | -8的立方根是2 |
16.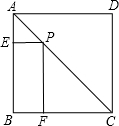 如图,P为正方形ABCD的对角线AC上任意一点,PE⊥AB于E,PF⊥BC于F,若AC=$\sqrt{2}$,则四边形PEBF的周长为( )
如图,P为正方形ABCD的对角线AC上任意一点,PE⊥AB于E,PF⊥BC于F,若AC=$\sqrt{2}$,则四边形PEBF的周长为( )
 如图,P为正方形ABCD的对角线AC上任意一点,PE⊥AB于E,PF⊥BC于F,若AC=$\sqrt{2}$,则四边形PEBF的周长为( )
如图,P为正方形ABCD的对角线AC上任意一点,PE⊥AB于E,PF⊥BC于F,若AC=$\sqrt{2}$,则四边形PEBF的周长为( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | 1 |
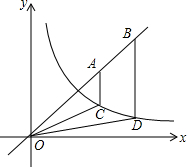 如图,点A,B为直线y=x上的两点,过A,B两点分别作y轴的平行线交双曲线$y=\frac{1}{x}$(x>0)于C,D两点.若BD=2AC.
如图,点A,B为直线y=x上的两点,过A,B两点分别作y轴的平行线交双曲线$y=\frac{1}{x}$(x>0)于C,D两点.若BD=2AC.