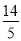题目内容
已知a≥2,m2﹣2am+2=0,n2﹣2an+2=0,m≠n,则(m﹣1)2+(n﹣1)2的最小值是( )
A. 6 B. 3 C. ﹣3 D. 0
A 【解析】已知m2﹣2am+2=0,n2﹣2an+2=0,可得m,n是关于x的方程x2﹣2ax+2=0的两个根,根据根与系数的关系可得m+n=2a,mn=2,再由(m﹣1)2+(n﹣1)2=m2﹣2m+1+n2﹣2n+1=(m+n)2﹣2mn﹣2(m+n)+2=4a2﹣4﹣4a+2=4(a﹣ )2﹣3,因a≥2,所以当a=2时,(m﹣1)2+(n﹣1)2有最小值,即(m﹣1)2+(n﹣1)...
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


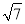 C. 0 D.
C. 0 D.