题目内容
15.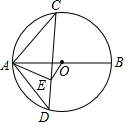 如图,AB是⊙O的直径,C是半圆的中点,连接CA,E是弦CD上一点,CE=CA,连接AD.
如图,AB是⊙O的直径,C是半圆的中点,连接CA,E是弦CD上一点,CE=CA,连接AD.(1)求证:AE平分∠BAD;
(2)连接OE,若AB=10,AD=6,求OE的长.
分析 (1)根据圆周角定理得到∠ADC=∠BAC,根据三角形的外角的性质证明即可;
(2)连接BD,作EF⊥BD于D,OG⊥BD于G,EH⊥OG于H,根据勾股定理求出BD,根据三角形的内心的概念得到E是△ADB的内心,根据勾股定理计算即可.
解答 (1)证明:∵C是半圆的中点,
∴$\widehat{AC}$=$\widehat{BC}$,
∴∠ADC=∠BAC,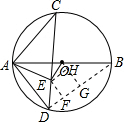
∵CE=CA,
∴∠CAE=∠CEA,又∠CEA=∠ADC+∠EAD,
∴∠BAE=∠DAE,即AE平分∠BAD;
(2)解:连接BD,作EF⊥BD于D,OG⊥BD于G,EH⊥OG于H,
由勾股定理得,BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=8,
∵C是半圆的中点,
∴DC平分∠ADB,又AE平分∠BAD,
∴E是△ADB的内心,
∴EF=$\frac{6+8-10}{2}$=2,
∵∠CDB=45°,
∴DF=EF=2,
∵OG⊥BD,
∴DG=$\frac{1}{2}$BD=4,
∴FG=2,
∴EH=FG=2,
∵OG是△BAD的中位线,
∴OG=$\frac{1}{2}$AD=3,
∴OH=1,
∴OE=$\sqrt{E{H}^{2}+O{H}^{2}}$=$\sqrt{5}$.
点评 本题考查的是圆周角定理、三角形的内心、三角形中位线定理,掌握三角形的内接圆的半径的求法是解题的关键.

练习册系列答案
相关题目
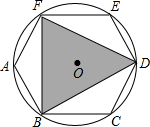 正六边形ABCDEF内接于⊙O,图中△FBD的面积为12$\sqrt{3}$,求⊙O的半径.
正六边形ABCDEF内接于⊙O,图中△FBD的面积为12$\sqrt{3}$,求⊙O的半径.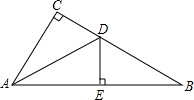 如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,若DE垂直平分AB.
如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,若DE垂直平分AB. 如图:在平面直角坐标系中,点O为坐标原点,△AOB的面积为18$\sqrt{3}$,∠ABO=60°,点C在OB上,OC=4,BC=2,动点P从A点出发沿射线AB以每秒2个单位的速度运动,连接OP.
如图:在平面直角坐标系中,点O为坐标原点,△AOB的面积为18$\sqrt{3}$,∠ABO=60°,点C在OB上,OC=4,BC=2,动点P从A点出发沿射线AB以每秒2个单位的速度运动,连接OP. 已知:如图,在正方形ABCD中,Q是CD中点,BP=3CP.
已知:如图,在正方形ABCD中,Q是CD中点,BP=3CP.