��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У���������x�ύ��A��B���㣨A��B����ࣩ����y�ύ�ڵ�C��0��4��������Ϊ��1��
����
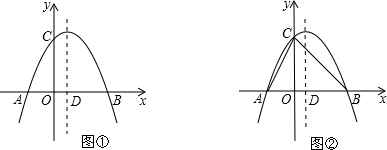
��1���������ߵĺ�����ϵʽ��
��2����ͼ�٣���������ߵĶԳ�����x�ύ�ڵ�D�����ڶԳ������ҳ���P��ʹ��CDPΪ���������Σ���ֱ��д���������������е�P�����ꣻ
��3����ͼ�ڣ�����AC��BC������E���߶�AB�ϵ�һ�����㣨���A��B���غϣ�������E��EF��AC���߶�BC�ڵ�F������CE���ǡ�CEF�����ΪS�����S�����ֵ����ʱE������꣮
| 9 | 2 |
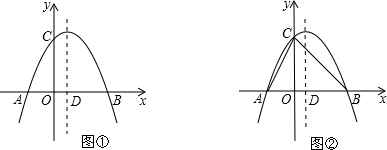
��1���������ߵĺ�����ϵʽ��
��2����ͼ�٣���������ߵĶԳ�����x�ύ�ڵ�D�����ڶԳ������ҳ���P��ʹ��CDPΪ���������Σ���ֱ��д���������������е�P�����ꣻ
��3����ͼ�ڣ�����AC��BC������E���߶�AB�ϵ�һ�����㣨���A��B���غϣ�������E��EF��AC���߶�BC�ڵ�F������CE���ǡ�CEF�����ΪS�����S�����ֵ����ʱE������꣮
��������1���������ߵĶ�����뵽�����ߵĶ���ʽ�еõ�y=a �� x-1��2+
��Ȼ����y�ύ�ڵ�C���뵽��ʽ�м�����ú����Ľ���ʽ��
��2�����õ��������ε����ʷֱ�ó�P������ꣻ
��3�������������x��Ľ������꣬Ȼ�����F��FM��OB�ڵ�M�����á�BEF�ס�BAC���ɵõ�������ϵʽS=-
x2+
x+
���䷽��������ֵ���Ӷ����E������꣮
| 9 |
| 2 |
��2�����õ��������ε����ʷֱ�ó�P������ꣻ
��3�������������x��Ľ������꣬Ȼ�����F��FM��OB�ڵ�M�����á�BEF�ס�BAC���ɵõ�������ϵʽS=-
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
���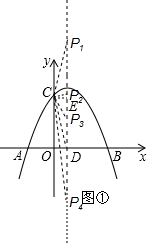 �⣺��1����Ϊ�����ߵĶ���Ϊ��1��
�⣺��1����Ϊ�����ߵĶ���Ϊ��1��
����
�����������ߵĺ�����ϵʽΪy=a �� x-1��2+
��
����������y�ύ�ڵ�C��0��4����
��a��0-1��2+
=4��
��ã�a=-
��
�����������ߵĺ�����ϵʽΪy=-
��x-1��2+
��
��2����ͼ�٣�����C��CE�ͶԳ����ڵ�E��
��CD=CP1ʱ���ߵ�C��0��4��������Ϊ��1��
����
��CD=
=
��DE=4��
��CP1=
��EP1=4��
��P1����������1��8����
��CD=DP2ʱ��P2������Ϊ����1��
����
��CP3=DP3ʱ��
��CP3=DP3=y��
��CE2+EP
=CP
��
��1+��4-y��2=y2��
��ã�y=
��
��P3����������1��
����
��CD=CP4ʱ��
P4����������1��-
����
������������������������P�������ǣ�
��1��
������1��-
������1��8������1��
����
��3����-
��x-1��2+
=0��
��ã�x1=-2��x2=4����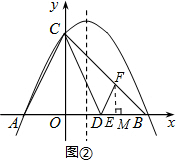
��������y=-
��x-1��2+
��x��Ľ���ΪA��-2��0����B��4��0����
����F��FM��OB�ڵ�M��
��EF��AC��
���BEF�ס�BAC��
=
��
�֡�OC=4��AB=6��
��MF=
��CO=
EB��
��E�����꣨x��0������EB=4-x��MF=
��4-x����
��S=S��BCE-S��BEF=
EB•CO-
EB•MF��
=
EB��OC-MF��=
��4-x��[4-
��4-x��]
=-
x2+
x+
=-
��x-1��2+3��
Qa=-
��0��
��S�����ֵ��
��x=1ʱ��S���ֵ=3��
��ʱ��E������Ϊ��1��0����
 �⣺��1����Ϊ�����ߵĶ���Ϊ��1��
�⣺��1����Ϊ�����ߵĶ���Ϊ��1��| 9 |
| 2 |
�����������ߵĺ�����ϵʽΪy=a �� x-1��2+
| 9 |
| 2 |
����������y�ύ�ڵ�C��0��4����
��a��0-1��2+
| 9 |
| 2 |
��ã�a=-
| 1 |
| 2 |
�����������ߵĺ�����ϵʽΪy=-
| 1 |
| 2 |
| 9 |
| 2 |
��2����ͼ�٣�����C��CE�ͶԳ����ڵ�E��
��CD=CP1ʱ���ߵ�C��0��4��������Ϊ��1��
| 9 |
| 2 |
��CD=
| 42+12 |
| 17 |
��CP1=
| 17 |
��P1����������1��8����
��CD=DP2ʱ��P2������Ϊ����1��
| 17 |
��CP3=DP3ʱ��
��CP3=DP3=y��
��CE2+EP
2 3 |
2 3 |
��1+��4-y��2=y2��
��ã�y=
| 17 |
| 8 |
��P3����������1��
| 17 |
| 8 |
��CD=CP4ʱ��
P4����������1��-
| 17 |
������������������������P�������ǣ�
��1��
| 17 |
| 17 |
| 17 |
| 8 |
��3����-
| 1 |
| 2 |
| 9 |
| 2 |
��ã�x1=-2��x2=4����

��������y=-
| 1 |
| 2 |
| 9 |
| 2 |
����F��FM��OB�ڵ�M��
��EF��AC��
���BEF�ס�BAC��
| MF |
| CO |
| EB |
| AB |
�֡�OC=4��AB=6��
��MF=
| BE |
| AB |
| 2 |
| 3 |
��E�����꣨x��0������EB=4-x��MF=
| 2 |
| 3 |
��S=S��BCE-S��BEF=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
=-
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
| 1 |
| 3 |
Qa=-
| 1 |
| 3 |
��S�����ֵ��
��x=1ʱ��S���ֵ=3��
��ʱ��E������Ϊ��1��0����
������������Ҫ�����˶��κ������ۺ����ͣ������漰����֪ʶ���������ߵĶ��㹫ʽ�������ε�����������йض�������ʱҪע����������������۽����

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD��
��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD�� ��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ�����
��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ����� ��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ
��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ ��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������
��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ��������� ��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��
��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��