题目内容
方程组
的解共有________组．
4
分析：本题中的两方程均含有|x+y|、|x|两项，故可用换元法先求出|x+y|及|x|的值，再根据绝对值的性质分别求出x、y的对应值即可．
解答：令|x+y|=u，|x|=v，则u+v=4，2u+3v=9，
解得v=1，u=3，
于是，x+y=±3，x=±1，
，
，
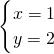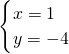或
共四组．
答案为：4．
点评：本题考查的是用换元法解二元一次方程组及绝对值的性质，分别设出|x+y|=u，|x|=v是解答此题的关键．
分析：本题中的两方程均含有|x+y|、|x|两项，故可用换元法先求出|x+y|及|x|的值，再根据绝对值的性质分别求出x、y的对应值即可．
解答：令|x+y|=u，|x|=v，则u+v=4，2u+3v=9，
解得v=1，u=3，
于是，x+y=±3，x=±1，
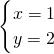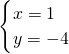，，或共四组．答案为：4．
点评：本题考查的是用换元法解二元一次方程组及绝对值的性质，分别设出|x+y|=u，|x|=v是解答此题的关键．
练习册系列答案
相关题目
方程组
的实数解共有（ ）
|
| A、1组 | B、2组 | C、3组 | D、4组 |
方程组
的解共有几组？（ ）
|
| A、l | B、2 | C、3 | D、≥4 |
的实数解共有
的解共有几组．