题目内容
如图,河中水中停泊着一艘小艇,王平在河岸边的A处测得∠DAC=α,李月在河岸边的B处测得∠DCA=β,如果A、C之间的距离为m,求小艇D到河岸AC的距离.
【答案】分析:首先作出河的宽度,过D作DB⊥AC与B点,则DB即为所求,在直角△ABD和直角△CDB中,根据三角函数用BD即可表示出AB和CB,根据AC=AB+CB即可得到一个关于BD的方程,即可求得BD的长
解答: 解:过点D作DB⊥AC于点B,设DB=x(1分)在Rt△ADB中,tan∠DAB=
解:过点D作DB⊥AC于点B,设DB=x(1分)在Rt△ADB中,tan∠DAB=
∴AB= =
= (4分)
(4分)
在Rt△CDB中,tan∠DCB=
∴BC= =
=
∵AB+BC=AC=m
∴ +
+ =m(8分)
=m(8分)
解得:x=
答:小艇D到河岸AC的距离为= (10分)
(10分)
点评:解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线
解答:
 解:过点D作DB⊥AC于点B,设DB=x(1分)在Rt△ADB中,tan∠DAB=
解:过点D作DB⊥AC于点B,设DB=x(1分)在Rt△ADB中,tan∠DAB=
∴AB=
 =
= (4分)
(4分)在Rt△CDB中,tan∠DCB=

∴BC=
 =
=
∵AB+BC=AC=m
∴
 +
+ =m(8分)
=m(8分)解得:x=

答:小艇D到河岸AC的距离为=
 (10分)
(10分)点评:解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线

练习册系列答案
相关题目
 如图,河中水中停泊着一艘小艇,王平在河岸边的A处测得∠DAC=α,李月在河岸边的B处测得∠DCA=β,如果A、C之间的距离为m,求小艇D到河岸AC的距离.
如图,河中水中停泊着一艘小艇,王平在河岸边的A处测得∠DAC=α,李月在河岸边的B处测得∠DCA=β,如果A、C之间的距离为m,求小艇D到河岸AC的距离.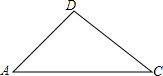 如图,河中水中停泊着一艘小艇,在岸边的A处测得∠DAC=45°,在岸边的C处测得∠DCA=30°,如果A、C之间的距离为100m,求小艇D到河岸AC的距离.
如图,河中水中停泊着一艘小艇,在岸边的A处测得∠DAC=45°,在岸边的C处测得∠DCA=30°,如果A、C之间的距离为100m,求小艇D到河岸AC的距离.