题目内容
如图，已知在△ABC中，内切圆I与边AB、AC分别相切于点D、E，点F是劣弧DE上一点，探索∠DFE与∠A的数量关系．考点：三角形的内切圆与内心
专题：
分析：连接IE和ID，利用四边形的内角和定理以及圆周角定理即可得到．
解答：
解：连接IE和ID．
∵AB和AC是圆的切线，
∴ID⊥AB，IE⊥AC．
∴∠ADI=∠AEI=90°，
∴∠A+∠DIE=180°，
∴∠DIE=180°-∠A．
∵∠DFE=
∠1，即∠1=2∠DFE，
又∠1+∠DIE=360°，
∴180°-∠A+2∠DFE=360°，
∴2∠DFE-∠A=180°．
解：连接IE和ID．∵AB和AC是圆的切线，
∴ID⊥AB，IE⊥AC．
∴∠ADI=∠AEI=90°，
∴∠A+∠DIE=180°，
∴∠DIE=180°-∠A．
∵∠DFE=
| 1 |
| 2 |
又∠1+∠DIE=360°，
∴180°-∠A+2∠DFE=360°，
∴2∠DFE-∠A=180°．
点评：本题考查了四边形的内角和定理以及圆周角定理，理解定理，正确作出辅助线是关键．
练习册系列答案
名校课堂系列答案
相关题目
下列事件发生的概率为0的是（ ）
| A、掷一枚均匀的硬币两次，至少有一次反面朝上 |
| B、今年冬天如皋会下雪 |
| C、掷两个均匀的骰子，朝上面的点数之和为1 |
| D、一个转盘被分成3个扇形，按红．白．黄排列，转动转盘，指针停在红色区域 |
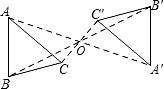如图，△ABC与△A′B′C′关于点O成中心对称，则下列结论不成立的是（ ）| A、点A与点A′是对称点 |
| B、BO=B′O′ |
| C、∠ACB=∠C′A′B′ |
| D、△ABC≌△A′B′C′ |
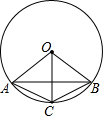如图，AB、AC、BC都是⊙O的弦，∠AOC=∠BOC．