题目内容
 如图,有一半径是1米的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形,用此扇形铁皮围成一个圆锥,该圆锥的底面圆的半径长为( )
如图,有一半径是1米的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形,用此扇形铁皮围成一个圆锥,该圆锥的底面圆的半径长为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:连接扇形的两个端点,则是直径,因而扇形的半径是2•sin45°=
,扇形的弧长l=
=
,圆锥的底面周长等于侧面展开图的扇形弧长,然后利用弧长公式计算.
| 2 |
90π•
| ||
| 180 |
| ||
| 2 |
解答:解:设底面圆的半径为r,则
=2πr,
∴r=
m
圆锥的底面圆的半径长为
米.
故选C.
| ||
| 2 |
∴r=
| ||
| 4 |
圆锥的底面圆的半径长为
| ||
| 4 |
故选C.
点评:本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
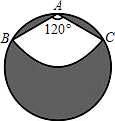 如图,有一直径是1米的圆形铁皮,要从中剪出一个圆心角是120°的扇形ABC,
如图,有一直径是1米的圆形铁皮,要从中剪出一个圆心角是120°的扇形ABC,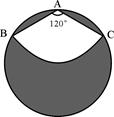
 如图,有一半径是1米的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形,用此扇形铁皮围成一个圆锥,该圆锥的底面圆的半径长为
如图,有一半径是1米的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形,用此扇形铁皮围成一个圆锥,该圆锥的底面圆的半径长为 米
米 米
米 米
米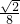 米
米
 米
米 米
米 米
米 米
米