题目内容
如图两个半圆相切于点C,大圆的弦AB切小圆于E,且AB∥CD,AB=6cm,则两个半圆所夹的阴影部分的面积为 cm2.
【答案】分析:过O作AB的一条垂线,垂足为M,则MB等于2/AB,根据勾股定理,即可求出阴影部分的面积为πOB2-πOM2,即πMB2.
解答: 解:过O作AB的一条垂线,垂足为M,
解:过O作AB的一条垂线,垂足为M,
∵AB∥CD,
∴OM=EF,
∵AB=6cm,
∴MB=3cm,
∴阴影部分的面积=(πOB2-πOM2)÷2,
∴S阴影= cm2.
cm2.
故答案为: cm2.
cm2.
点评:本题主要考查了圆的面积、垂径定理、切线的性质、勾股定理,解题的关键是作好辅助线,构建直角三角形.
解答:
 解:过O作AB的一条垂线,垂足为M,
解:过O作AB的一条垂线,垂足为M,∵AB∥CD,
∴OM=EF,
∵AB=6cm,
∴MB=3cm,
∴阴影部分的面积=(πOB2-πOM2)÷2,
∴S阴影=
 cm2.
cm2.故答案为:
 cm2.
cm2.点评:本题主要考查了圆的面积、垂径定理、切线的性质、勾股定理,解题的关键是作好辅助线,构建直角三角形.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
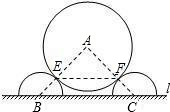 半径为4米的⊙A构成.点B、C分别是两个半圆的圆心,⊙A分别与两个半圆相切于点E、F,BC长为8米.求EF的长.
半径为4米的⊙A构成.点B、C分别是两个半圆的圆心,⊙A分别与两个半圆相切于点E、F,BC长为8米.求EF的长. 如图两个半圆相切于点C,大圆的弦AB切小圆于E,且AB∥CD,AB=6cm,则两个半圆所夹的阴影部分的面积为
如图两个半圆相切于点C,大圆的弦AB切小圆于E,且AB∥CD,AB=6cm,则两个半圆所夹的阴影部分的面积为 如图两个半圆相切于点C,大圆的弦AB切小圆于E,且AB∥CD,AB=6cm,则两个半圆所夹的阴影部分的面积为________cm2.
如图两个半圆相切于点C,大圆的弦AB切小圆于E,且AB∥CD,AB=6cm,则两个半圆所夹的阴影部分的面积为________cm2.