题目内容
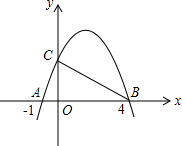 如图,已知抛物线和x轴交于两点A、B,和y轴交于点C,已知A、B两点的横坐标分别为-1,4,△ABC是直角三角形,∠ACB=90°,则此抛物线顶点的坐标为________.
如图,已知抛物线和x轴交于两点A、B,和y轴交于点C,已知A、B两点的横坐标分别为-1,4,△ABC是直角三角形,∠ACB=90°,则此抛物线顶点的坐标为________.
( ,
, )
)
分析:根据点A、B的横坐标求出OA、OB的长,再根据△AOC和△COB相似,利用相似三角形对应边成比例列式求出OC的长度,然后写出点C的坐标,然后设抛物线解析式为y=a(x+1)(x-4),把点C的坐标代入求出a的值,再整理成顶点式形式,然后写出顶点坐标即可.
解答: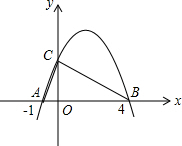 解:∵A、B两点的横坐标分别为-1,4,
解:∵A、B两点的横坐标分别为-1,4,
∴OA=1,OB=4,
∵∠ACB=90°,
∴∠CAB+∠ABC=90°,
∵CO⊥AB,
∴∠ABC+∠BCO=90°,
∴∠CAB=∠BCO,
又∵∠AOC=∠BOC=90°,
∴△AOC∽△COB,
∴ =
= ,
,
即 =
=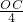 ,
,
解得OC=2,
∴点C的坐标为(0,2),
∵A、B两点的横坐标分别为-1,4,
∴设抛物线解析式为y=a(x+1)(x-4),
把点C的坐标代入得,a(0+1)(0-4)=2,
解得a=- ,
,
∴y=- (x+1)(x-4)=-
(x+1)(x-4)=- (x2-3x-4)=-
(x2-3x-4)=- (x-
(x- )2+
)2+ ,
,
∴此抛物线顶点的坐标为( ,
, ).
).
故答案为:( ,
, ).
).
点评:本题考查了二次函数综合题型,主要利用了相似三角形的判定与性质,待定系数法求二次函数解析式,利用相似三角形对应边成比例求出OC的长得到点C的坐标是解题的关键,利用抛物线交点式形式更简单.
 ,
, )
)分析:根据点A、B的横坐标求出OA、OB的长,再根据△AOC和△COB相似,利用相似三角形对应边成比例列式求出OC的长度,然后写出点C的坐标,然后设抛物线解析式为y=a(x+1)(x-4),把点C的坐标代入求出a的值,再整理成顶点式形式,然后写出顶点坐标即可.
解答:
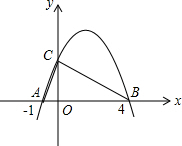 解:∵A、B两点的横坐标分别为-1,4,
解:∵A、B两点的横坐标分别为-1,4,∴OA=1,OB=4,
∵∠ACB=90°,
∴∠CAB+∠ABC=90°,
∵CO⊥AB,
∴∠ABC+∠BCO=90°,
∴∠CAB=∠BCO,
又∵∠AOC=∠BOC=90°,
∴△AOC∽△COB,
∴
 =
= ,
,即
 =
=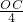 ,
,解得OC=2,
∴点C的坐标为(0,2),
∵A、B两点的横坐标分别为-1,4,
∴设抛物线解析式为y=a(x+1)(x-4),
把点C的坐标代入得,a(0+1)(0-4)=2,
解得a=-
 ,
,∴y=-
 (x+1)(x-4)=-
(x+1)(x-4)=- (x2-3x-4)=-
(x2-3x-4)=- (x-
(x- )2+
)2+ ,
,∴此抛物线顶点的坐标为(
 ,
, ).
).故答案为:(
 ,
, ).
).点评:本题考查了二次函数综合题型,主要利用了相似三角形的判定与性质,待定系数法求二次函数解析式,利用相似三角形对应边成比例求出OC的长得到点C的坐标是解题的关键,利用抛物线交点式形式更简单.

练习册系列答案
相关题目
 13、如图,已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=-1,P1(x1,y1),P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且-1<x1<x2,x3<-1,则y1,y2,y3的大小关系为
13、如图,已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=-1,P1(x1,y1),P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且-1<x1<x2,x3<-1,则y1,y2,y3的大小关系为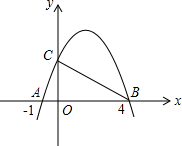 如图,已知抛物线和x轴交于两点A、B,和y轴交于点C,已知A、B两点的横坐标分别为-1,4,△ABC是直角三角形,∠ACB=90°,则此抛物线顶点的坐标为
如图,已知抛物线和x轴交于两点A、B,和y轴交于点C,已知A、B两点的横坐标分别为-1,4,△ABC是直角三角形,∠ACB=90°,则此抛物线顶点的坐标为 和直线
和直线 .我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的有 (
)
.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的有 (
)
 和直线
和直线 .我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.
.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.
