题目内容
【题目】如图1，
，
，
.
绕着边
的中点
旋转，
，
分别交线段
于点
.
（1）观察：①如图2、图3，当
或
时，
________
（填“
”，“
”或“
”）
②如图4，当
时，________（填“”或“”）
（2）猜想：如图1，当
时，________，证明你所得到的结论.
（3）如果
，请求出
的度数和
的值.
【答案】（1）①= ②＞ （2）>，见解析 （3）15°；
【解析】
（1）①根据直角三角形斜边中线的性质可得CD=AD=BD=
AB，分
或
时两种情况，可得AM=0或CK=0，即可得出
；
②由∠BDC=60°可知∠ADC=120°，根据∠CDF=30°可求出∠ADM=30°，可得AM=DM，CK=KD，根据三角形的三边关系即可得答案；
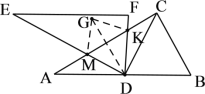
（2）如图，作点C关于FD的对称点G，连接GK，GM，GD．根据直角三角形斜边中线的性质及等腰三角形的性质可证明
，利用SAS可证明△ADM≌△GDM，根据全等三角形的性质可得GM=AM，根据三角形三边关系即可得答案；
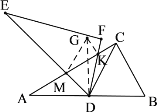
（3）根据勾股定理的逆定理求得∠GKM=90°，由轴对称的性质可得∠CKG=90°，∠FKC=∠CKG=45°，根据三角形的外角定理，可得∠CDF=15°；在Rt△GKM中，∠MGK=∠DGK+∠MGD=∠A+∠ACD=60°，可得∠GMK=30°，利用余弦的定义可得
=cos30°，即可得答案．
（1）①∵在
中，
是
的中点，∠ACB=90°，∠A=30°，
∴
，
，
∴
，
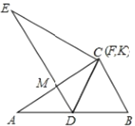
如图，当
时，
，点A与点M重合，
∵AD=CD，
∴CK=MK，
∵AM=0，
∴AM+CK=MK，
如图，当∠CDF=0°时，
∵△ABC≌△EDF，
∴DF=BC，∠EDF=∠B=60°，
∴DF=CD，即点C与点F、K重合，
∵∠ACD=30°，∠EDF=60°，
∴∠CDM=90°，
∴AM=MK，
∵CK=0，
∴
综上所述：，
故答案为：=
②由①，得
，
，
∴∠ADC=120°，
∵
，
，
，
∴
，
∴
，
∴
∴在
中
（两边之和大于第三边）.
（2）作点
关于
的对称点
，连接
，
，
，则
，
，
∵是的中点，
∴
，
∴
，
，
∴
，
∵，
∴
，
∴，
在△ADM和△GDM中，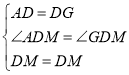
，
∴
，
∴
，
∵
，
∴
（3）如图，由（2），得，
∵
，
∴
，
∴
，
∵点关于的对称点为，
∴
，
，
由（1）可知：
，
∵
，
∴
，
在
中，
，
∴
，
∴GK=MG，
∴MK=
=GM，
∴
，
∴
，
综上可得：
的度数为
，的值为．
