题目内容
△ABC的三边为a、b、c，且满足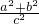
+3.25=2×
，则△ABC是
- A.直角三角形
- B.等腰三角形
- C.等边三角形
- D.以上答案都不对
B
分析：将等式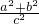+3.25=2×，化简得4（a-c）2+（2b-3c）2=0，解得a=c，即可．
解答：由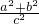+3.25=2×，
化简得4（a-c）2+（2b-3c）2=0，
由4（a-c）2=0和（2b-3c）2=0，
解得：a=c则△ABC是等腰三角形，
故选B．
点评：此题主要考查学生对完全平方式和非负数的性质：偶次方的理解和掌握，主要是将已知等式化简成完全平方式，再利用非负数的性质：偶次方，求得a=c，这是此题的关键，也是难点，因此这是一道难题．
分析：将等式
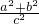+3.25=2×，化简得4（a-c）2+（2b-3c）2=0，解得a=c，即可．解答：由
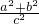+3.25=2×，化简得4（a-c）2+（2b-3c）2=0，
由4（a-c）2=0和（2b-3c）2=0，
解得：a=c则△ABC是等腰三角形，
故选B．
点评：此题主要考查学生对完全平方式和非负数的性质：偶次方的理解和掌握，主要是将已知等式化简成完全平方式，再利用非负数的性质：偶次方，求得a=c，这是此题的关键，也是难点，因此这是一道难题．
练习册系列答案
高中必刷题系列答案
相关题目
若三角形ABC的三边为a，b，c，满足条件：a2+b2+c2+338=10a+24b+26c，则这个三角形最长边上的高为（ ）
| A、8 | ||
B、
| ||
C、
| ||
D、
|
探究题
如图，以Rt△ABC的三边为直角边分别向外作等腰直角三角形．若AB=5，则图中阴影部分的面积为（ ）