题目内容
13.探索与思考.让我们规定一种新运算$|\begin{array}{l}{a}&{c}\\{b}&{d}\end{array}|$=a•d-b•c,例如$|\begin{array}{l}{3}&{4}\\{2}&{5}\end{array}|$=3×5-2×4=7,则$|\begin{array}{l}{3}&{\frac{1}{2}}\\{2}&{\frac{2}{3}}\end{array}|$=1,$|\begin{array}{l}{-2}&{-\frac{1}{2}}\\{3}&{\frac{3}{2}}\end{array}|$=-$\frac{3}{2}$.
分析 原式利用题中的新定义计算即可得到结果.
解答 解:原式=3×$\frac{2}{3}$-2×$\frac{1}{2}$=2-1=1;原式=-2×$\frac{3}{2}$+3×$\frac{1}{2}$=-$\frac{3}{2}$,
故答案为:1;-$\frac{3}{2}$
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
3.下列叙述中,正确的是( )
| A. | 相等的两个角是对顶角 | |
| B. | 过一点有且只有一条直线与已知直线平行 | |
| C. | 垂直于同一条直线的两直线平行 | |
| D. | 从直线外一点到这条直线上的各点连结的所有线段中,垂线段最短 |
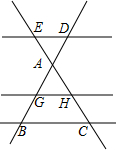 如图,ED∥GH∥BC.
如图,ED∥GH∥BC.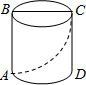 如图:一个圆柱的底面周长为16cm,高为6cm,BC是上底面的直径,一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,求蚂蚁爬行的最短路程(要求画出平面图形).
如图:一个圆柱的底面周长为16cm,高为6cm,BC是上底面的直径,一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,求蚂蚁爬行的最短路程(要求画出平面图形).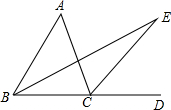 如图所示,∠ACD是△ABC的外角,∠A=40°,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.
如图所示,∠ACD是△ABC的外角,∠A=40°,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E. 如图,CD是△ABC的角平分线,∠A=55°,∠B=70°,则∠1=27.5°.
如图,CD是△ABC的角平分线,∠A=55°,∠B=70°,则∠1=27.5°.