题目内容
16.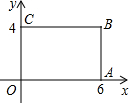 如图,矩形OABC的顶点O在坐标原点,点B的坐标是(6,4),如果矩形OA'B'C'与矩形OABC关于点O位似,且矩形OA'B'C'的面积等于矩形OABC面积的$\frac{1}{9}$,那么点B'的坐标是(2,$\frac{4}{3}$)或(-2,-$\frac{4}{3}$).
如图,矩形OABC的顶点O在坐标原点,点B的坐标是(6,4),如果矩形OA'B'C'与矩形OABC关于点O位似,且矩形OA'B'C'的面积等于矩形OABC面积的$\frac{1}{9}$,那么点B'的坐标是(2,$\frac{4}{3}$)或(-2,-$\frac{4}{3}$).
分析 根据面积比等于相似比的平方得到位似比为$\frac{1}{3}$,由图形得到点B的坐标,根据注意在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标比等于±k解答即可.
解答 解:∵矩形OA′B′C′与矩形OABC关于点O位似,矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{9}$,
∴矩形OA′B′C′与矩形OABC的位似比是$\frac{1}{3}$,
∵点B的坐标是(6,4),
∴点B′的坐标是(2,$\frac{4}{3}$)或(-2,-$\frac{4}{3}$),
故答案为(2,$\frac{4}{3}$)或(-2,-$\frac{4}{3}$).
点评 本题考查了位似变换的性质,掌握位似比等于相似比,其对应的面积比等于相似比的平方是解题的关键,注意在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标比等于±k.

练习册系列答案
相关题目
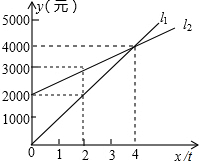 L1反应了某公司产品的销售收入与销售量的关系,L2反应了该公司产品的销售成本与销售量的关系,根据图中信息填空:
L1反应了某公司产品的销售收入与销售量的关系,L2反应了该公司产品的销售成本与销售量的关系,根据图中信息填空: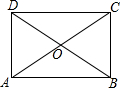 如图,?ABCD中,AB=8,AC=10,BC=6,求?ABCD的面积.
如图,?ABCD中,AB=8,AC=10,BC=6,求?ABCD的面积.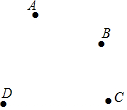 如图所示,平面上有四个点A、B、C、D,根据下列语句画图:
如图所示,平面上有四个点A、B、C、D,根据下列语句画图: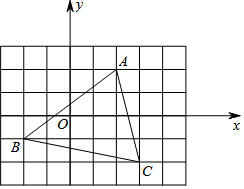 如图,△ABC在平面直角坐标系中:
如图,△ABC在平面直角坐标系中: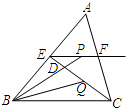 如图所示,在△ABC中,BC=4,E、F分别是AB、AC上的点,且EF∥BC,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当CQ=$\frac{1}{3}$CE时,EP+BP=8.
如图所示,在△ABC中,BC=4,E、F分别是AB、AC上的点,且EF∥BC,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当CQ=$\frac{1}{3}$CE时,EP+BP=8.