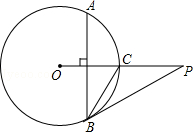
题目内容
如图,已知P是⊙O外一点,PO交圆O于点C,OC=CP=2,弦AB⊥OC,劣弧AB的度数为120°,连接PB.
(1)求BC的长;
(2)求证:PB是⊙O的切线.

考点:
切线的判定;等边三角形的判定与性质;垂径定理.
分析:
(1)首先连接OB,由弦AB⊥OC,劣弧AB的度数为120°,易证得△OBC是等边三角形,则可求得BC的长;
(2)由OC=CP=2,△OBC是等边三角形,可求得BC=CP,即可得∠P=∠CBP,又由等边三角形的性质,∠OBC=60°,∠CBP=30°,则可证得OB⊥BP,继而证得PB是⊙O的切线.
解答:
(1)解:连接OB,
∵弦AB⊥OC,劣弧AB的度数为120°,
∴弧BC与弧AC的度数为:60°,
∴∠BOC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴BC=OC=2;
(2)证明:∵OC=CP,BC=OC,
∴BC=CP,
∴∠CBP=∠CPB,
∵△OBC是等边三角形,
∴∠OBC=∠OCB=60°,
∴∠CBP=30°,
∴∠OBP=∠CBP+∠OBC=90°,
∴OB⊥BP,
∵点B在⊙O上,
∴PB是⊙O的切线.

点评:
此题考查了切线的判定、等边三角形的判定与性质以及等腰三角形的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
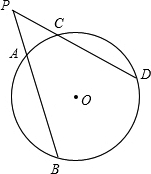 如图,已知P是⊙O外任意一点,过点P作直线PAB,PCD,分别交⊙O于点A,B,C,D.求证:∠P=
如图,已知P是⊙O外任意一点,过点P作直线PAB,PCD,分别交⊙O于点A,B,C,D.求证:∠P=
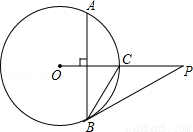
 (2013•湖州)如图,已知P是⊙O外一点,PO交圆O于点C,OC=CP=2,弦AB⊥OC,劣弧AB的度数为120°,连接PB.
(2013•湖州)如图,已知P是⊙O外一点,PO交圆O于点C,OC=CP=2,弦AB⊥OC,劣弧AB的度数为120°,连接PB. 如图,已知A是⊙O外一点,B是⊙O上一点,AO的延长线交⊙O于C,连结BC.已知∠C=22.5°,∠BAC=45°,判断AB是否为⊙O的切线并说明理由.
如图,已知A是⊙O外一点,B是⊙O上一点,AO的延长线交⊙O于C,连结BC.已知∠C=22.5°,∠BAC=45°,判断AB是否为⊙O的切线并说明理由.